Теоретические исследования.

Если обозначить среднее давление на подошву абсолютно жесткого круглого фундамента (рисунок 4) через р_т,то давление в лю­бой точке подошвы будет равно [13]

,

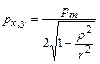(18)

где r — радиус подошвы круглого жесткого фундамента;

r — расстояние от центра круглой подошвы до любой точки на граничной плоскости (при r < r).

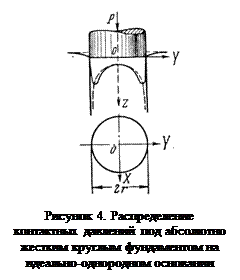Приведенное решение показывает, что к краям жесткого фундамента давления увеличиваются и по периметру достигают бесконечно большой величины. Последнее обстоятельство не может быть в действительности, так как величина напряже­ний ограничена «пределом текучести» материала массива. По периметру жесткого фундамента возникнут остаточные пласти­ческие деформации, и давления будут значительно меньше теоретических.

На рисунке 4 приведены теоретическая кривая (пунктир) рас­пределения давлений под жестким круглым фундаментом и кривая (сплошная), ограниченная пределом «текучести» грунта для того же фундамента.

Если жесткий цилиндрический фундамент нагружен силой Р, приложенной с эксцен­трицитетом е, то, согласно решению, полученному К. Е. Егоро­вым, величина давлений под подошвой фундамента определяется по формуле [14]

,

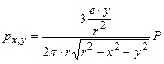(19)

где Р — нагрузка на весь фундамент;

r — радиус подошвы фундамента;

х, у — координаты рассматриваемой точки.

Распределение давлений по подошве ленточного абсолютно жесткого фундамента определяется выражением [14]

,

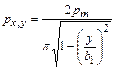(20)

где р_т — среднее давление на единицу площади подошвы фундамента;

у — расстояние по горизонтали от середины фундамента до рассматриваемой точки;

b₁— полуширина фундамента.

Очевидно, что и в обоих последних случаях к краям жесткого фундамента давления увеличиваются и достигают беспредельно большой величины.