Энтальпия и полезная внешняя работа

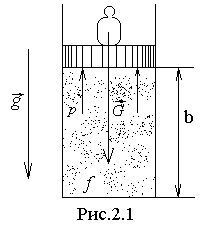Пусть в вертикально расположенном цилиндре под поршнем находится газ (рис.2.1). На поршень давит груз весом G = M_грg. Если груз вместе с поршнем неподвижны, значит, на поршень снизу действует давление со стороны газа, равное 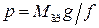, где f – площадь поршня. Это выражение может быть записано в виде 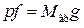. Умножив левую и правую части этого равенства на высоту b положения поршня от дна цилиндра, получим 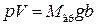. Произведение 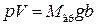есть потенциальная энергия поршня с грузом в поле тяжести Земли, удерживающая газ в заданном объеме V, рассчитанная по отношению к положению дна цилиндра. Можно показать, что и в общем случае потенциальная энергия оболочки, удерживающей систему, равняется произведению pV. При этом система не обязательно должна быть заключена в физическую оболочку.

Если в качестве системы рассматривать не только газ, но и груз с поршнем, то энергия такой расширенной системы будет складываться из внутренней энергии газа и потенциальной энергии поршня с грузом. Эта энергия и называется энтальпией термодинамической системы и обозначается буквой H: .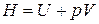

Применим к I закону термодинамики преобразование Лежандра:

.

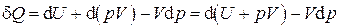Здесь под знаком полного дифференциала появляется новая функция состояния – энтальпия (старое название – теплосодержание). Таким образом, первое начало термодинамики может быть записано в двух эквивалентных формах:

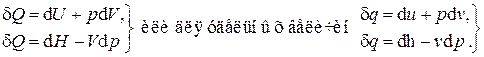
В результате этого преобразования появилось слагаемое 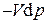, имеющее смысл бесконечно малого количества некоторой работы :

.

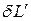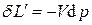Интеграл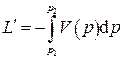

носит название полезной внешней работы (или располагаемой работы). Выясним смысл полезной внешней работы. Работа 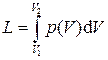, которую можно назвать работой изменения объема, представляет собой работу, совершаемую системой против внешних сил. Часть этой работы, называемая работой проталкивания L_пр, затрачивается на изменение потенциальной энергии оболочки и может быть вычислена как разность

.

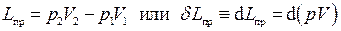Дифференциал этой работы, очевидно, полный. Разность бесконечно малых количеств работы и работы проталкивания равна

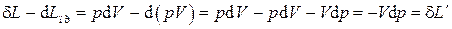
или после интегрирования .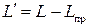

Таким образом, полезная внешняя работа есть разность между работой термодинамической системы и работой проталкивания.

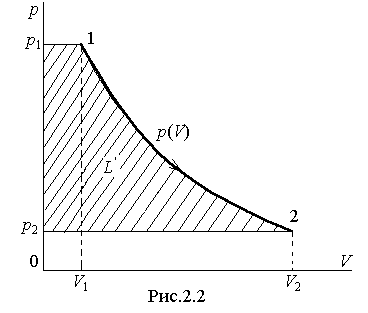Графически количество полезной внешней работы L^', соответствует площади слева от кривой зависимости p(V) в координатахp – V (рис.2.2).

Таким образом, первое начало термодинамики для простых систем может быть записано в виде

.

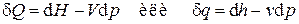Полный дифференциал удельной энтальпии в переменных T и p имеет вид

.

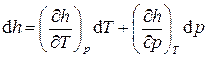Лекция 5