Дифференциальные уравнения термодинамики

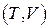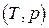Запишем внутреннюю энергию U и энтальпию H системы как функции переменных и соответственно. Тогда полные дифференциалы этих функций запишутся в виде

,

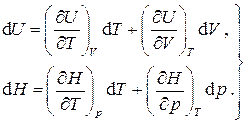где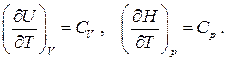

Частные производные при дифференциалах 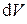и 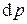находятся из того факта, что дифференциал энтропии является полным. Имеем из уравнений Гиббса:

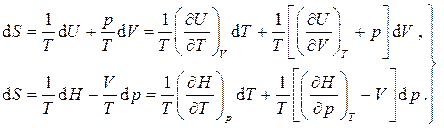
Из равенства перекрестных производных для полного дифференциала получаем

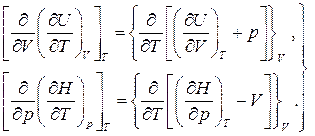
Вычисление частных производных с учетом независимости порядка дифференцирования для непрерывных функций приводит к следующему результату:

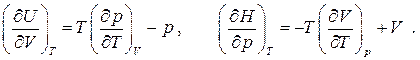
Полные дифференциалы внутренней энергии, энтальпии и энтропии принимают вид

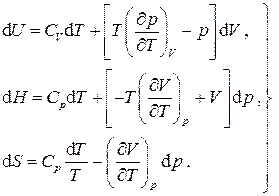
Используя полноту этих дифференциалов, т.е. равенство перекрестных производных, находим зависимость теплоемкостей 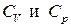от объема и давления соответственно:

.

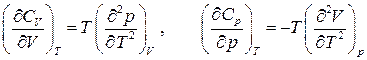Функции, частные производные от которых пропорциональны теплоемкостям системы, называются калорическими функциями, а уравнения – калорическими уравнениями состояния. В частности, калорическими функциями являются внутренняя энергия U(T,V) и энтальпия H(T, p).