Энтропия идеального газа

Запишем первый закон термодинамики для идеального газа:

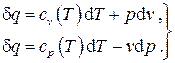
Каждая из этих дифференциальных форм не является полным дифференциалом, однако в случае идеального газа легко проверить, что умножение их на функцию 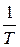превращает их в полные дифференциалы.

Учтя уравнение состояния идеального газа 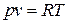, имеем

.

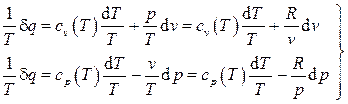Вычисление перекрестных производных дает

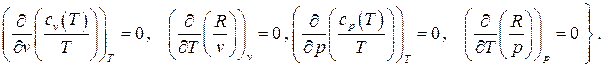Равенство перекрестных производных говорит о том, что дифференциал 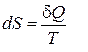[U7] является полным, а величина

.

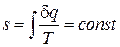есть некоторая новая функция состояния системы, которая по предложению немецкого ученого Р. Клаузиуса [U8] была названа энтропией.

Тогда выражение для количества теплоты может быть записано в форме, аналогичной выражению для работы, т.е. как произведение некоторого потенциала (в данном случае температуры T) на изменение некоторой "координаты"(в данном случае энтропии s):

,

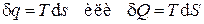а количество теплоты в некотором процессе определится интегралом

.

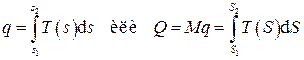Использование понятия энтропии позволяет ввести в рассмотрение термодинамическую диаграмму T – s, в которой количество теплоты определится площадью под кривой процесса, т.е. графическим изображением зависимости температуры от энтропии .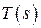

Для идеального газа

.

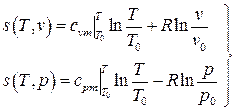Здесь учтено, что энтропия принимается равной нулю при нормальных физических условиях (НФУ).

Физический смысл энтропии.

Классическая термодинамика, опираясь на экспериментальный факт невозможности построения вечного двигателя второго рода, позволяет приписать любой равновесной термодинамической системе некоторую функцию состояния – энтропию 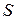, которая выступает в роли сопряженной переменной по отношению к термодинамической температуре 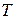. Энтропию неравновесной термодинамической системы классическая термодинамика определить не может, она позволяет только утверждать, что если система переходит из одного равновесного состояния в другое равновесное состояние необратимым образом, то разность энтропий конечного и начального состояний будет больше суммы приведенных теплот в течение процесса. В применении к адиабатическому процессу

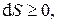
т.е. в адиабатически изолированных системах энтропия не уменьшается.

Лекция 6