Безынерционные динамические модели

1.2.1.1. Модель тренда. Широко применяется в задачах прогнозирования и сглаживания временных рядов [6, 45]. Для случая 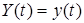, 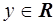модель записывается в виде

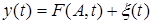, (1.4)

где 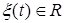— случайный процесс, 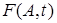— известная с точностью до вектора параметров A функция времени.

Модель (1.4) может быть как линейной, так и нелинейной по 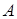, а время 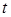непрерывным или дискретным.

1.2.1.2. Регрессионная модель. Имеет вид

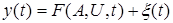, (1.5)

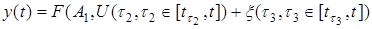, (1.6)

где 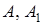— векторы параметров, 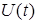— вектор входа (управления), 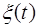— случайное возмущение.

Модель (1.6) является обобщением статической регрессионной модели (1.5). Уравнение (1.6) при 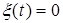и дискретном 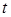получило название модели скользящего среднего], а при 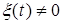представляет собой модель скользящего среднего с динамической спецификацией для стохастической части.

Как и в (1.4), так и (1.6) предполагается, что структура оператора 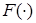задана с точностью до вектора неизвестных параметров 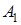. Поэтому все выше сказанное в пункте 1.2.1.1 относительно свойств 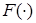справедливо и в этом случае.

Таким образом, безынерционные динамические модели (1.6) характеризуются временным распределением (лагом) переменных .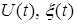

Уравнение (1.5) используется в системах управления статическими объектами [51, 56].