Задача обслуживания заявок на одном приборе

Основные понятия. Классификация

Одну и ту же задачу оптимизации можно решить различными методами. Их может быть несколько десятков, поэтому их разбивают на классы. Методы делятся на прямые и непрямые.

Непрямой метод – такой, в котором экстремальная задача сводится к некоторой другой математической задаче, например, алгебраической – нахождение стационарных точек. Мы, в основном, будем рассматривать прямые методы.

Пусть дана задача:

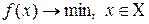(1)

и пусть задано начальное приближение .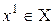

В прямых методах строится последовательность:

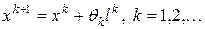(2)

в которой 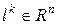– направление итерации, 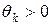– шаг в этом направлении. Шаг и направление выбирают, чтобы выполнялось неравенство:

.

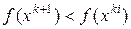Иногда 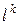и 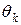можно подобрать, так, чтобы последовательность 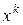являлась минимизирующей. Обычно в каждом методе задаётся малая величина 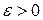, которая служит для прекращения итерации и определяет точность метода. Прекращение итерации обычно осуществляется с помощью проверки одного из условий:

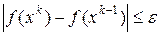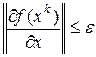1 2 3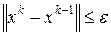

Если условие прекращения итерации выполнено, то 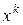принимается в качестве приближённого решения задачи.

Методы делятся на детерминированные и стохастические. Есл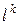и и 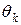вычисляются по определённым формулам, то метод называется детерминированным, а если для их построения используются механизмы теории вероятности, то метод называется стохастическим.

Метод называется методом 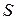-го порядка, если для вычисления направления и шага итерации используются производные от параметров задачи до 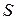-ой включительно. Если 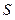=0, то такой метод называется методом поиска или перебора.

Методы делятся на конечные и бесконечные. Метод называется конечным, если за конечное число итераций удаётся в точности найти оптимальный план.

Методы делятся на точные и приближённые. В точных методах на итерациях преобразуются планы, то есть 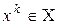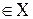. В приближённых методах 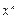могут лежать в 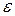-окрестности планов.

Методы также различают по использованию ресурсов ЭВМ, объёму памяти, быстроте нахождения решения и так далее.

МЕТОДЫ ПОИСКА

Обычно методами поиска решаются задачи:

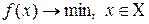(1)

дискретного программирования, то есть, когда либо конечное, либо счётное множество в 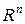. Предполагается, что задано начальное приближение 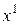. Затем по некоторому правилу из множества 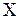извлекаются планы 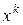и подставляются в целевую функцию. Лучший план запоминается. Если множество, 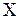– конечно, то можно перебрать все планы и найти оптимальный. Если – счётное множество, то оптимальный план найти удаётся не всегда, так как полный перебор произвести нельзя. В силу того, что на перебор затрачиваются ресурсы (в основном временные), то в методах поиска возникает проблемы сокращения объёма перебираемых планов и таким образом, чтобы оно, тем не менее, позволило бы построить достаточно хорошее приближение к решению.

Определение. Пусть удалось построить некоторое количество планов 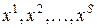к некоторой итерации. Тогда рекордом итерации называют число 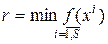. А тот из построенных планов, на котором достигается рекорд, называется рекордным планом.

Методы перебора применяют также и к непрерывным задачам (обычно на первых итерациях). При этом предварительно непрерывное множество 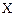превращается в дискретное с помощью введения некоторой решётки в 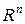. Затем по узлам этой решётки осуществляется перебор, находится лучший из таких планов. К этому плану возможно применение методов более высокого порядка.

Задача обслуживания заявок на одном приборе

Это простейшая задача теории расписания.

Постановка задачи. Имеется некоторый прибор (станок, аппарат и так далее) и имеется 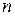заявок для обслуживания на этом приборе. Для каждой заявки указано 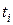– время обслуживания и 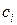– штраф за единицу времени ожидания в очереди, 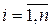. Требуется указать оптимальную последовательность облуживания заявок на приборе, такую, чтобы суммарный штраф был минимальным.

Математическая модель. Пусть 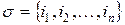– последовательность обслуживания заявок на приборе, при которой первой обслуживается заявка с номером 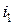, второй – 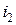и так далее, последней – с номером 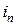. Это и будет план задачи. Множество всех планов обозначим через 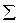– это множество перестановок из 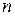чисел. Тогда ясно, что всего планов будет 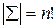. Поэтому для этой задачи возможен полный перебор. Каждому плану 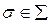поставим в соответствие штраф 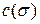так что:

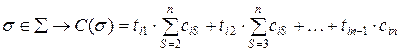
Задача обслуживания принимает вид:

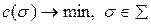(2)

Хотя возможен полный перебор, но он не рационален. Оптимальный план можно получить методом вариаций.

Определение. Простейшей вариацией перестановки 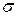называют такую перестановку 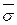, у которой по сравнению с 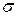переставлены местами две соседние заявк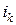и и .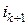

, .

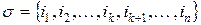
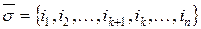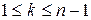Подсчитаем, на сколько изменится штраф при переходе от 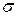к 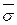. Имеем:

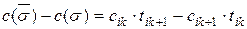
Предположим, что 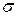оказалась оптимальной перестановкой 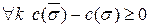. Это значит, что

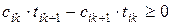
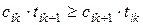
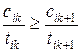
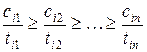(3)

(3) − необходимое условие оптимальности 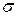, а так как у задачи существует оптимальный план, то это необходимое условие будет и достаточным, то есть любая последовательность, которая удовлетворяет (3) будет оптимальной.

Согласно критерию оптимальности 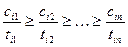в первую очередь должны обслуживаться заявки с наибольшим относительным штрафом на единицу времени ожидания. Ясно, как без перебора найти оптимальную последовательность: для каждого 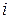подсчитать 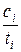, полученные числа упорядочить по убыванию.

Рассмотрим частный случай, когда для всех заявок штраф одинаковый.

.

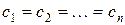Тогда сократив в (3) числитель на эту общую величину, получим критерий оптимальности:

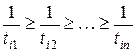, (4)

согласно которому в первую очередь должны обслуживаться заявки с наименьшим временем исполнения.

Пример. Если в качестве прибора рассмотреть приёмную начальника, а в качестве заявок – посетителей, записавшихся к нему на приём. Для того чтобы суммарно посетители меньше страдали в очереди, начальник должен принимать, тех, у кого вопросы мелкие.