Задача целочисленного линейного программирования
Рассмотрим задачу в канонической форме с дополнительным условием:
переменные должны быть целыми числами
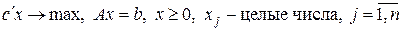
Как правило, производственная задача, в которой продукция неделимая, является целочисленной. Однако при решении непрерывной задачи оптимальный план зачастую имеет дробные компоненты. Его округление до целых не всегда подходит. Метод ветвей и границ впервые был применён к целочисленной линейной задаче. На нулевой итерации решается непрерывная задача в канонической форме и получается оптимальный план 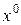 для неё. Если он оказался целочисленным, то он естественно будет оптимальным и для целочисленной задачи. В противном случае число
для неё. Если он оказался целочисленным, то он естественно будет оптимальным и для целочисленной задачи. В противном случае число 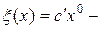 оценка сверху (задача максимизации).
оценка сверху (задача максимизации).
Затем множество 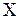 дробиться на два подмножества по некоторой компоненте
дробиться на два подмножества по некоторой компоненте 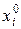 , которая оказалась дробной в
, которая оказалась дробной в 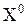 .
.
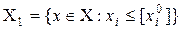
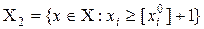
ясно, что 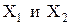 не пересекаются, а в объединении дают множество
не пересекаются, а в объединении дают множество 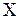 . Переходим к первой итерации.
. Переходим к первой итерации.
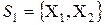 . Для нахождения
. Для нахождения 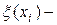 верхней границы,
верхней границы, 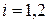 решается задача
решается задача 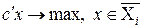 , где
, где 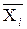 – это
– это 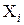 , в котором отброшено условие целочисленности.
, в котором отброшено условие целочисленности.
Замечание. Эту непрерывную задачу удобно решать, продолжая решение исходной задачи двойственным симплекс-методом, используя уже построенную симплекс-таблицу. Для этого достаточно ввести в симплекс-таблицу неравенство, которое используется для построения 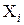 (приведённое к каноническому виду).
(приведённое к каноническому виду).
Разбиением множеств 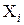 на два новых осуществляется таким же образом, как и на нулевой итерации (по оптимальному плану непрерывной задачи на этом множестве).
на два новых осуществляется таким же образом, как и на нулевой итерации (по оптимальному плану непрерывной задачи на этом множестве).
И так далее.
Дата добавления: 2021-07-22; просмотров: 433;











