Метод ветвей и границ. Общая схема Задача целочисленного линейного программирования

Метод ветвей и границ является одним из самых популярных методов перебора, который позволяет значительно сокращать объём перебираемых планов за счёт исключения бесперспективных подмножеств планов, то есть таких, которые заведомо не содержат решения.

Метод применяют к задачам:

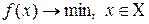, (1)

для которых выполняются два предположения:

1. множество планов 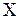и любое его подмножество 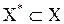можно дробить (ветвить) на более мелкие, (причём дробление должно быть таким, чтобы во-первых, попарное пересечение более мелких подмножеств было пустым, а во-вторых, в объединении они должны давать дробимые подмножества).

2. для множества 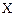и для любого его подмножества 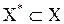может быть вычислена эффективная нижняя грань значений целевой функций на нём, то есть для 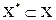можно построить число 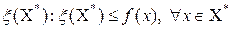(5)

Общая схема

В методе на каждой итерации строится список 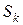из перспективных подмножеств, одно из которых, по крайне мере содержит оптимальный план. На нулевой итерации 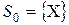. Вычисляем оценку итерации 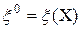, рекорд итерации .

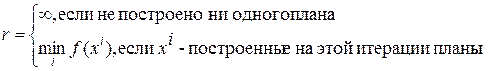Вычисляем разность 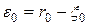. Возможны случаи:

1. 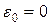. В этом случае рекордный план будет оптимальным планом задачи, так как на нём достигалась нижняя граница.

2. 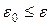, где 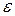- малое положительное число, заданная точность вычисления. В этом случае рекордный план можно взять в качестве 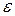- оптимального, то есть приближённого решения задачи (1).

3. 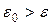. Тогда заданная точность не достигнута. Переходим к первой итерации. Для этого в соответствие с первым предположением 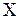ветвим на более мелкие. Для каждого вычисляем границу по второму предположению, и бесперспективные подмножества отбрасываем, а перспективные включаем в список для первой итерации.

Определение. Пусть на некоторой итерации есть подмножество 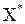и вычислен рекорд 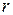. Тогда множество будет перспективным, если 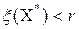. Если 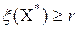, то, очевидно, на нём нет планов, лучших, чем рекордный и, ветвь можно отсечь, это подмножество будет бесперспективным.

Пусть 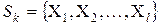– список перспективных подмножеств 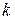-ой итерации. Вычисляем оценку итерации 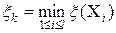. Вычисляем рекорд итерации .

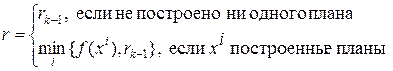Вычисляем разность .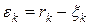

Совершаем анализ:

4. если 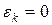, то построен оптимальный план. Записываем ответ.

5. если 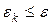, то построен 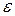-оптимальный план. Записываем ответ.

6. если 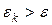, то переходим к 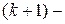ой итерации. Для этого выбираем из 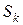наиболее перспективное подмножество ( с наименьшей нижней границей) и дробим его по первому предположению. В 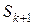включаем перспективные подмножества из вновь полученных дроблением и остальных подмножеств множества .

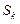И так далее.

Ясно, что на итерациях 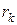уменьшаются, а 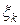увеличиваются (чем мельче подмножество, тем точнее можно для неё построить границу). Следовательно, числа 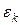будут уменьшаться и, в конце концов, метод ветвей и границ позволит, решить задачу (1).

Замечание 2. Слово «эффективная» во втором предположении означает, что нижняя граница 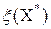не сильно отличается от точной нижней. Чем точнее строится оценка, тем быстрее сходится метод ветвей и границ.