Свойства параллельного проецирования

МЕТОДЫ И СВОЙСТВА ПРОЕЦИРОВАНИЯ

Центральное проецирование

Суть метода заключается в том, что предметы (точки, прямые, плоскости, поверхности), находящиеся в пространстве, проецируются на некоторую плоскость лучами, выходящими из одной точки.

Изображение предметов при помощи центрального проецирования обладает хорошей наглядностью, но по такому изображению трудно определить истинную форму и размеры предмета. Проецирование широко применяется в изобразительном искусстве (при построении перспективы), в кинематографии.

При составлении машиностроительных чертежей пользуются другим методом проецирования – параллельным.

Параллельное проецирование

Существо метода заключается в том, что проецирующие лучи выходят из точки, которая удалена от плоскости проекции в бесконечность. В этом случае проецирующие лучи можно считать параллельными между собой.

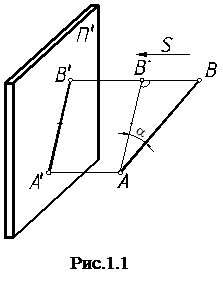
Параллельное проецирование отрезка АВ на плоскость П' представлено на рис. 1.1. Лучи, выходящие из точек А и В, параллельны между собой и параллельны заданному лучу .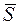

Свойства параллельного проецирования

Параллельное проецирование обладает большими возможностями решения графических задач на основе таких свойств: проекцией точки является точка, прямой – прямая линия, параллельных прямых – параллельные прямые. Если точка делит отрезок прямой в некотором отношении, то и проекции отрезка находятся в таком же отношении.

В зависимости от направления проецирующего луча по отношению к плоскости П' параллельное проецирование может быть косоугольным (φ ≠ 90°) или прямоугольным (φ = 90°) – ортогональным.

Все машиностроительные чертежи выполняются на основе ортогонального проецирования, так как в этом случае легко устанавливается соотношение между длиной отрезка и его проекциями и соблюдается свойство о проецировании прямого угла плоскости. Читается это свойство так: прямой угол проецируется на плоскость в общем случае с искажением, но одна из сторон пря-
мого угла параллельна плоскости проекций – в этом случае проекция прямого угла – 90°. Это свойство является важным при решении геометрических задач.

Рассмотренные методы проецирования предмета на одну плоскость проекций позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его чертежи. Однако обратная задача – по данному чертежу воспроизвести оригинал – не решается однозначно. В этом случае говорят – “чертеж необратим”. Для получения обратимых чертежей существуют различные методы дополнения однокартинного чертежа.