Взаимное расположение прямой и плоскости
Прямая принадлежит плоскости, если имеет две общие точки или одну общую точку и параллельна какой-либо прямой, лежащей в плоскости. Пусть плоскость на чертеже задана двумя пересекающимися прямыми. В данной плоскости требуется построить две прямые m и n в соответствии с этими условиями (Г (а 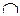 b)) (рис. 4.5).
b)) (рис. 4.5).
 Р е ш е н и е. 1. Произвольно проводим m2, так как прямая принадлежит плоскости, отмечаем проекции точек пересечения ее с прямыми а и b и определяем их горизонтальные проекции, через 11 и 21 проводим m1.
Р е ш е н и е. 1. Произвольно проводим m2, так как прямая принадлежит плоскости, отмечаем проекции точек пересечения ее с прямыми а и b и определяем их горизонтальные проекции, через 11 и 21 проводим m1.
2. Через точку К плоскости проводим n2║m2  и n1║m1.
и n1║m1.
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в плоскости.
Пересечение прямой и плоскости. Возможны три случая расположения прямой и плоскости относительно плоскостей проекций. В зависимости от этого определяется точка пересечения прямой и плоскости.
 Первый случай – прямая и плоскость – проецирующего положения. В этом случае точка пересечения на чертеже имеется (обе ее проекции), ее нужно только обозначить.
Первый случай – прямая и плоскость – проецирующего положения. В этом случае точка пересечения на чертеже имеется (обе ее проекции), ее нужно только обозначить.
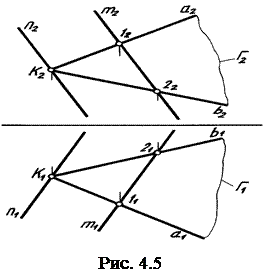
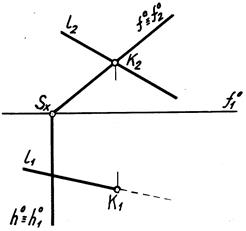
П р и м е р. На чертеже задана плоскость следами Σ (h0  f 0) – горизонтально проецирующего положения – и прямая l – фронтально проецирующего положения. Определить точку их пересечения (рис. 4.6).
f 0) – горизонтально проецирующего положения – и прямая l – фронтально проецирующего положения. Определить точку их пересечения (рис. 4.6).
Точка пересечения на чертеже уже есть – К(К1К2).
Второй случай – или прямая, или плоскость – проецирующего положения. В этом случае на одной из плоскостей проекций проекция точки пересечения уже имеется, ее нужно обозначить, а на второй плоскости проекций – найти по принадлежности.
а б
Рис. 4.7
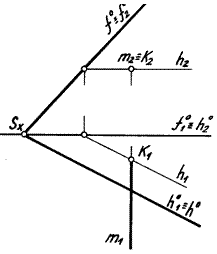
 П р и м е р ы. На рис. 4.7, а изображена плоскость следами фронтально проецирующего положения и прямая l – общего положения. Проекция точки пересечения К2 на чертеже уже имеется, а проекцию К1 необходимо найти по принадлежности точки К прямой l. На
П р и м е р ы. На рис. 4.7, а изображена плоскость следами фронтально проецирующего положения и прямая l – общего положения. Проекция точки пересечения К2 на чертеже уже имеется, а проекцию К1 необходимо найти по принадлежности точки К прямой l. На
рис. 4.7, б плоскость общего положения, а прямая m – фронтально проецирующего, тогда К2 уже есть (совпадает с m2), а К1 нужно найти из условия принадлежности точки К плоскости. Для этого через К проводят
прямую (h – горизонталь), лежащую в плоскости.
Третий случай – и прямая, и плоскость – общего положения. В этом случае для определения точки пересечения прямой и плоскости необходимо воспользоваться так называемым посредником – плоскостью проецирующей. Для этого через прямую проводят вспомогательную секущую плоскость. Эта плоскость пересекает заданную плоскость по линии. Если эта линия пересекает заданную прямую, то есть точка пересечения прямой и плоскости.
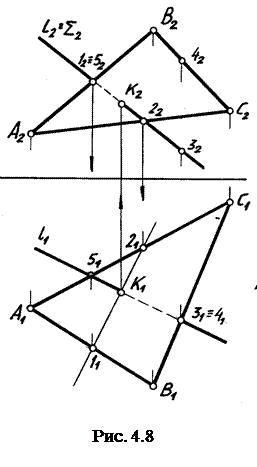
П р и м е р ы. На рис. 4.8 представлены плоскость треугольником АВС – общего положения – и прямая l – общего положения. Чтобы определить точку пересечения К, необходимо через l провести фронтально проецирующую плоскость Σ, построить в треугольнике линию пересечения Δ и Σ (на чертеже это отрезок 1,2), определить К1 и по принадлежности – К2. Затем определяется видимость прямой l по отношению к треугольнику по конкурирующим точкам. На П1 конкурирующими точками взяты точки 3 и 4. Видима на П1 проекция точки 4, так как у нее координата Z больше, чем у точки 3, следовательно, проекция l1 от этой точки до К1 будет невидима.
 На П2 конкурирующими точками взяты точка 1, принадлежащая АВ, и точка 5, принадлежащая l. Видимой будет точка 1, так как у нее координата Y больше, чем у точки 5, и следовательно, проекция прямой l2 до К2 невидима.
На П2 конкурирующими точками взяты точка 1, принадлежащая АВ, и точка 5, принадлежащая l. Видимой будет точка 1, так как у нее координата Y больше, чем у точки 5, и следовательно, проекция прямой l2 до К2 невидима.
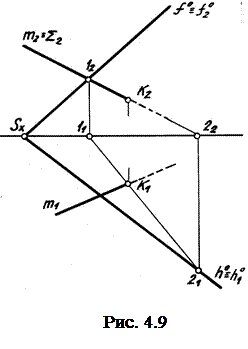
На рис. 4.9 изображены плоскость общего положения (задана следами) и прямая m также общего положения. Чтобы определить точку пересечения m и плоскости, надо через m2 провести Σ2 – фронтально проецирующую плоскость, построить линию пересечения двух плоскостей (отрезок 1,2), отметить К1 и по принадлежности этой точки прямой l определить К2.
Дата добавления: 2017-04-05; просмотров: 1843;











