Критическая скорость, критическое давление, максимальный расход
Исследование формул (8.8) и (8.10) показывает, что с уменьшением давления р2 увеличиваются значения v2 и w. Но в начале адиабатного расширения скорость w увеличивается быстрее, чем объем v2, и расход М. растет. Достигнув некоторого максимума при β = р2/p1 = 0,5, расход М начинает уменьшаться. Это происходит потому, что при дальнейшем
уменьшении отношения p2/p1 скорость w растет медленнее, чем объем v2. При р2 = 0 w 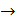 wмакс, a v2
wмакс, a v2 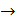
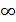 , следовательно, М
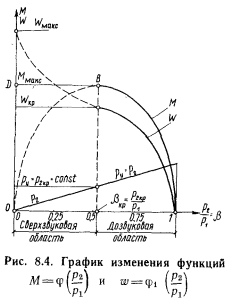
, следовательно, М  0 и кривая M = j (β) принимает форму параболы (см. рис. 8.4).
0 и кривая M = j (β) принимает форму параболы (см. рис. 8.4).
Опыт, однако, показывает, что изменение расхода М после достижения максимума Ммакс при дальнейшем уменьшении р2 и вместе с ним β следует не по пунктирной линии ВО, а по горизонтали BD. Такое расхождение с формулой (8.10) объясняется тем, что, понижая постепенно давление р2, будем получать давление в устье сопла, равное р2, только до значения p2кр/p1 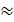 0,5. При дальнейшем уменьшении этого отношения, т. е. при снижении давления р2 в среде, куда втекает газ, давление в устье сопла ру не понижается, а остается постоянным, происходит как бы «запирание» сопла. Это остающееся постоянным в устье сопла давление, которое нельзя понизить, уменьшив давление в среде, куда происходит истечение, называется критическим и обозначается р2кр, а отношение p2кр/p1 обозначается βKp.
0,5. При дальнейшем уменьшении этого отношения, т. е. при снижении давления р2 в среде, куда втекает газ, давление в устье сопла ру не понижается, а остается постоянным, происходит как бы «запирание» сопла. Это остающееся постоянным в устье сопла давление, которое нельзя понизить, уменьшив давление в среде, куда происходит истечение, называется критическим и обозначается р2кр, а отношение p2кр/p1 обозначается βKp.
Формула (8.10) дает соответствующее действительности значение расхода, если в ней и при р2/p1 < βKp рассматривать р2 как давление в устье сопла, а не как давление среды, в которую втекает газ. Вместе с этим в устье сопла остаются постоянными и удельный объем v2|кр, и скорость истечения wкр, несмотря на уменьшение давления среды р2.
Секундный расход М, достигающий при βKp максимального значения Ммакс, также остается постоянным и не зависит от дальнейшего понижения р2. Поэтому, начиная от βKp, действительные кривые расхода и скорости (см. рис. 8.4) изобразятся прямыми, параллельными оси абсцисс.
Рассмотренное явление объясняется тем, что устанавливающаяся при β = βкр критическая скорость истечения является максимальной и превысить ее для суживающихся сопел не представляется возможным [см. уравнение (8.17)]. Следовательно:
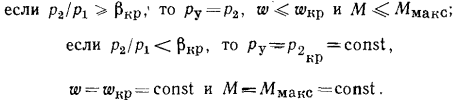
Обобщая все сказанное, устанавливаем в соответствии с уравнением (8.10), что расход М газа данных параметров зависит от сечения f и давления в устье сопла ру.
Для определения βкр нужно найти отношение р2/p1, при котором функция М = j(р2/p1) достигает максимального значения. Для этого нужно взять первую производную от этой функции, приравнять ее к нулю и найти то значение аргумента р2/р1, при котором функция М будет иметь экстремум.
В формуле (8.10) переменной является разность
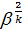 —
— 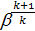
{M = f 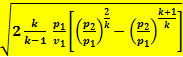 (8.10) }
(8.10) }
Поэтому в целях сокращения математических преобразований первую производную берем от этого выражения и приравниваем ее к нулю, в результате чего получаем:
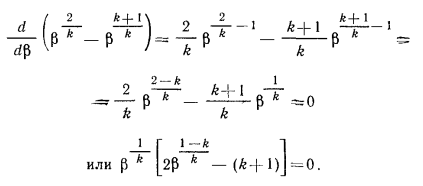
Но 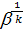 ¹ 0, ибо для этого или р2 = 0, или р1 = ¥, чего практически не бывает. Тогда может быть равен нулю лишь второй множитель, т. е.
¹ 0, ибо для этого или р2 = 0, или р1 = ¥, чего практически не бывает. Тогда может быть равен нулю лишь второй множитель, т. е.
2 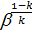 = k + 1; 2
= k + 1; 2 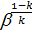 =
= 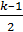 , или
, или 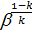 =
= 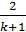 ,
,
И окончательно
bкр = 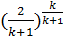 (8.11)
(8.11)

Формула (8.11) показывает, что bкр = р2кр/р зависит только от природы газа или пара, вытекающего через сопло, так как для каждого рабочего тела имеется свое значение k: для двухатомных газов k = 1,4, ркр = 0,528, р2кр = 0,528р1; для перегретого пара k =1,3, bкр = 0,546, р2кр = 0,546 р1.
{ w 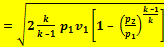 (8.8) }
(8.8) }
Подставляя в формулу (8.8) значение bкр из уравнения (8.11), получим выражение для определения wKP:
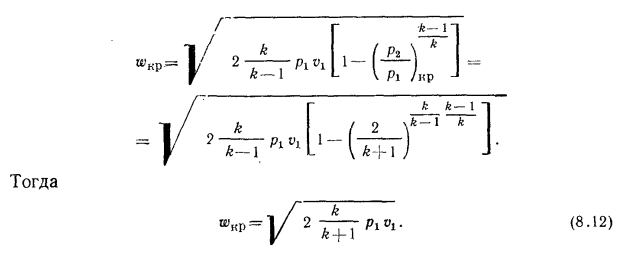
Тогда
wкр = 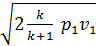 (8.12)
(8.12)
Из формулы следует, что критическая скорость вполне определяется начальным состоянием газа и показателем адиабаты k. В частности, для двухатомных газов wкр = 1,08 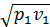 , или wкр = 1,08
, или wкр = 1,08 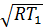 т. е. скорость wкр возрастает с увеличением начальной температуры и для разных газов различна. Например, для воздуха при t = 200 °С
т. е. скорость wкр возрастает с увеличением начальной температуры и для разных газов различна. Например, для воздуха при t = 200 °С
wкр = 1,08 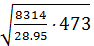 = 398 м/с,
= 398 м/с,
а при t = 1000 °С
wкр =1,08 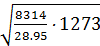 = 650 м/с.
= 650 м/с.
Для перегретого пара wкр = 1,06 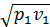 . Во всех формулах р в Н/м2, w в м/с, а
. Во всех формулах р в Н/м2, w в м/с, а 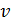 в м3/кг.
в м3/кг.
Лекция №5.
Дата добавления: 2021-07-22; просмотров: 595;











