Определение работы, скорости и расхода газа в процессе истечения

Изучение закономерностей движения газов и паров но каналам имеет чрезвычайно большое значение для рассмотрения рабочих процессов ряда машин, аппаратов и приборов.

В промышленности строительных материалов теория газового потока нашла широкое применение при проектировании установок для раздува силикатных расплавов в минеральное волокно, эжекторных установок для перекачки горючих газов, а также при решении вопросов, связанных с созданием инжекционных газовых горелок, форсунок для сжигания жидкого и твердого пылевидного топлива и других агрегатов, устройство которых основано на преобразовании энергии давления в кинетическую энергию движения рабочего тела.

Термодинамическая теория газового потока позволяет определить скорость истечения газа, его секундный расход и основные закономерности профилирования сопел и диффузоров.

Для исследований процесса истечения задача может быть сформулирована так.

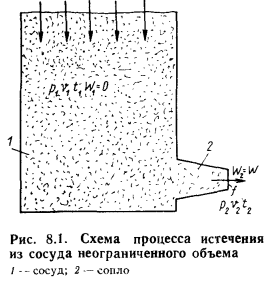
Имеется сосуд 1 неограниченной вместимости, где находится рабочее тело — газ или пар с параметрами состояния p₁, t₁, v₁ (рис. 8.1). Рабочее тело вытекает в среду с давлением р₂ < р₁ за счет разности давлений

р₁ - р₂ через отверстие в стенке сосуда. Удельный объём и температуру газа в среде с давлением р₂ обозначим соответственно через р₂, v₂ и t₂. Чтобы придать нужное направление струе рабочего тела, вытекающей из сосуда, к отверстию с наружной поверхности стенки сосуда приставляют насадки 2, называемые соплами, имеющие цилиндрическую или чаще форму суживающегося усеченного конуса (коноидальное сопло)*. Выходное сечение сопла называется устьем.

Обозначим площадь поперечного сечения устья сопла f и скорость струи газа или пара, выходящей из устья сопла, w₂, скорость газа, втекающего в сосуд, — w₁. Обычно эта скорость очень мала по сравнению с w₂, и поэтому при практических расчетах ею можно пренебречь, т. е. считают w₁= 0, и тогда w₂ обозначают просто w.

В соответствии с уравнением (2.6) имеем dq = du + dA' + (dw²/2). С другой стороны, по уравнению (2.4) dq = du+ dA (где dA = pdv —элементарная работа расширения, совершаемая газом). Тогда (т.к. dq= dq)

dA = dA' + (dw²/2)

Или dA₀ = (dw²/2) = dA – dA' (8.1)

и

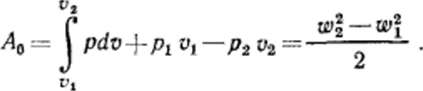
(8.2)

* Такое сопло иначе называется конфузором. Канал, в котором происходит обратный процесс, т. е. увеличивается давление газа и уменьшается скорость его течения, называется диффузором.

Величина А₀ называется работой, которой мы располагаем в процессе истечения, и численно равна алгебраической сумме внешней работы газа и работы проталкивания, или приращению кинетической энергии при истечении газа. Эта работа может быть использована в машинах непосредственно или превращена в другие виды энергии. Например, в паровых турбинах пар, пропускаемый через криволинейные каналы рабочего колеса со значительной скоростью, полученной в результате расширения, снижает скорость и вследствие уменьшения внешней кинетической энергии создает вращающий момент на валу турбины, т. е. совершает работу.

Так как по уравнению (2.8')

q = i₂ – i₁ + (w₂² — w₁²)/ 2 = i₂ – i₁ + А₀ (2.8')

то

А₀ = (w₂² — w₁²)/2 = q + i₁ – i₂

Теоретически процесс истечения является изоэнтропным, т. е. совершается без теплообмена газа с внешней средой (q = 0). Тогда последнее равенство примет вид

(w₂² — w₁²)/2 = А₀ = i₁ – i₂. (8.3)

Из формулы (8.3) следует, что при адиабатном процессе истечения газа А₀ определяется уменьшением его энтальпии. Подставляя в уравнение (8.2) значение работы для адиабатного процесса расширения идеального газа, по уравнению (3.15) получим:

(A = 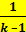(p₁v₁ – p₂v₂) – (3.15) — работа в адиабатном процессе.)

А₀ = 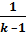(p₁v₁ – p₂v₂) +p₁v₁ – p₂v₂ = (p₁v₁ – p₂v₂)( 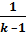+ 1) =

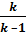= (p₁v₁ – p₂v₂)

или

А₀ = 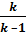p₁v₁ [1– (р₂/р₁)^(k-1/k)] (8.4)

Таким образом, при адиабатном процессе истечения идеального газа

А₀ в k раз больше работы расширения газа. Уравнение (8.1 dA₀ = (dw²/2) = dA – dA') можно переписать так (см. §2.3):

dA₀ = dA — dA' = pdv – d(pv) = – vdp.

тогда

A₀ = – ò^р2_р1 vdp (8.5)

и

dA₀ = dw²/2 = wdw = — vdp. (8.6)

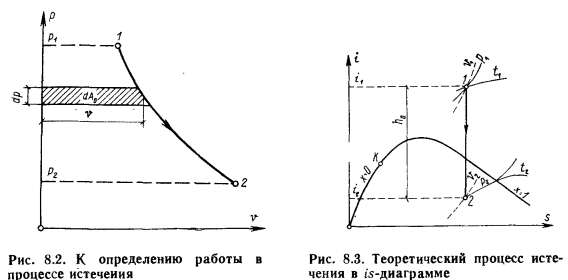
Для бесконечно малого перепада давления dp элементарную работу dA₀ подсчитывают как площадь прямоугольника с основанием v и высотой dp (рис. 8.2).

Равенство (8.6) отражает основные особенности течения газов. Оно показывает, что при движении газа знаки dw и dp всегда противоположны. Иначе говоря, если газ (или пар) при движении по каналу расширяется (давление при dq = 0 падает), его скорость и кинетическая энергия будут увеличиваться, и наоборот, если при движении газа по каналу давление будет возрастать (газ при dq = 0 сжимается), то его скорость и кинетическая энергия будут уменьшаться.

Для адиабатного течения газа работа А₀ в соответствии с формулой
(8.3) может быть определена через энтальпию, т. е. А₀ = i₁ — i₂ и графически А₀ в is-диаграмме (рис. 8.3) будет изображаться отрезком h₀, который соответствует перепаду энтальпий i₁ – i₂.

При w₁ = 0 скорость истечения w₂ = w может быть определена из уравнения (8.3):

(w₂² — w₁²)/2 = А₀ = i₁ – i₂. (8.3)

w = 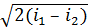(8.7)

где i выражено в Дж/кг, w — в м/с.

В частном случае, если i измерено в кДж/кг, формула (8.7) принимает вид

w = 44,72 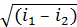(8.7')

а если, как это часто бывает, i измерено в ккал/кг, то

w = 91,53 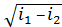(8.7'')

Полученную формулу особенно удобно использовать для определения скорости истечения водяного пара с помощью is-диаграммы.

Для идеального газа по уравнению (8.4 А₀ = 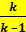p₁v₁ [1– (р₂/р₁)^(k-1/k)]) скорость истечения w может быть выражена также через начальные параметры газа р₁ и v₁ и давление среды р₂ куда происходит истечение:

A₀ = 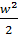= 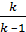p₁v₁ ,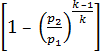

откуда

w 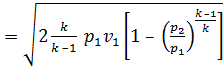(8.8)

где, р [Н/м²] , v [м³/кг] , w [м/с].

Если принять p₁v₁ = RT₁, то

w 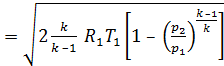(8.8')

откуда следует, что скорость истечения w растет с увеличением начальной температуры газа T₁ и при прочих равных условиях будет иметь большую величину для более легких газов с большим значение газовой постоянной R. По формуле (8.8) можно определять и скорость истечения водяного пара, если считать, что k = 1,3 — для перегретого пара и k = 1,135 — для сухого насыщенного пара.

Количество рабочего тела (пара или газа), вытекающего из сопла в 1 с (см. рис. 8.1), определяют из соотношения

M = V₂/v₂,

где V₂ — секундный объем вытекающего газа; v₂ — удельный объем газа при давлении р₂.

Поскольку

V₂ = fw,

то

М = fw/v₂. (8.9)

Подставляя в полученное равенство значение скорости по уравнению (8.8) и значение v₂ из уравнения адиабаты, равное v₂ = v₁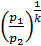

получим:

M = f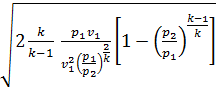

Или

M = f 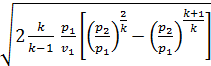(8.10)

Для определения секундного расхода пара следует пользоваться непосредственно формулой (8.9), находя w по формуле (8.7), a v₂ – по is-диаграмме (см. рис. 8.3).

Из формул (8.8) и (8.10) следует, что w и M зависят от отношения р₂/р₁. Очевидно, при р₂/р₁ = 1 w = 0 и M = 0, т. е. при равенстве давлений р₁ и р₂ истечения не будет. При уменьшении давления р₂, а следовательно, и отношения р₂/р₁ при постоянном давлении р₁ скорость w и расход газа М увеличиваются. Если предположить, что р₂ = 0, т. е. что истечение происходит в среду, где полный вакуум, то следовало бы ожидать, что расход должен быть максимальным. Однако по формуле (8.10) расход получается равным нулю. Этот результат представляется неправдоподобным. Для объяснения его проанализируем формулу (8.10). С этой целью построим графики зависимости M = j (р₂ /p₁) и w = j(р₂/р₁) причем для краткости написания отношение р₂/р₁ будем обозначать буквой β.По оси абсцисс отложим β от 0 до 1 (рис. 8.4), а по оси ординат — соответствующее значение М.

Лекция №4.