Определение критической скорости, критического давления, максимального расхода водяного пара

Для водяного пара wкр может быть определена также по is-диаграмме, если в формуле (8.7) (w = 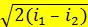 ) вместо i2 подставить значение i2кр, определяемое по is-диаграмме как точка пересечения адиабаты с критической изобарой р2кр (рис. 8.5), т. е.
) вместо i2 подставить значение i2кр, определяемое по is-диаграмме как точка пересечения адиабаты с критической изобарой р2кр (рис. 8.5), т. е.
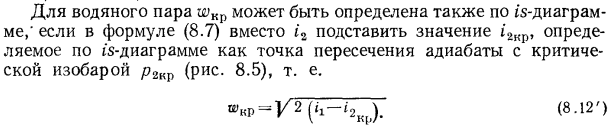
Очевидно, что на создание кинетической энергии вытекающей струи рабочего тела в этом случае расходуется не всё теплопадение h0, а лишь часть его 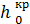 = i1 –i2кр. Оставшаяся часть h0 —
= i1 –i2кр. Оставшаяся часть h0 — 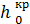 = i2кр — i2 представляет собой потери на вихревые движения по выходе струи из устья сопла.
= i2кр — i2 представляет собой потери на вихревые движения по выходе струи из устья сопла.
Если подставить значение bкр = 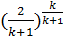 в формулу (8.10),
в формулу (8.10),
{M = f 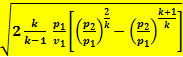 (8.10) }
(8.10) }
получим уравнение для определения максимального секундного расхода Ммакс:
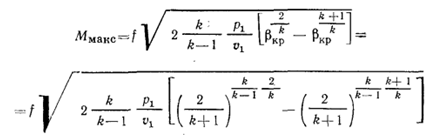
и окончательно
Ммакс = f× 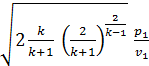 (8.13)
(8.13)
Или
Ммакс = f×y 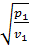 (8.13¢)
(8.13¢)
Где, y = 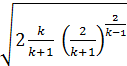
определяется только природой газа, т. е. величиной k. В частности, для двухатомных газов при k = 1,4 y = 0,68; для перегретого пара при k = 1,3 y = 0,665.
Рассмотрим связь скорости движения с геометрической формой сопла. Из условия неразрывности движения в соответствии с уравнением (8.9) имеем Mv = fw. Дифференцируя это равенство, находим fdw + wdf = Mdv и, разделив на fw получим
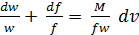 , но
, но 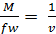 , тогда
, тогда
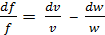 (а)
(а)
Уравнение (а) представляет собой условие неразрывности потока в дифференциальной форме. Величину dv/v найдем из уравнения адиабаты
pvk = const. Дифференцируя это уравнение, получим
kpvk - 1 dv + vkdp = 0 и, разделив на vk, найдем
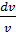 = –
= – 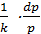 (б)
(б)

Из курса физики известно, что
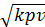 = wзв (8.15)
= wзв (8.15)
где wзв — скорость звука в среде с параметрами p и v.
Для установления характерных особенностей течения газов скорость звука, представляющая собой скорость распространения упругих деформаций, имеет большое значение. Из формулы (8.15) видно, что wзв зависит от параметров состояния р и v и природы газа k. Для идеальных газов pv = RT, тогда
wзв = 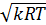 (8.15¢)
(8.15¢)
В частности, для воздуха k = 1,4, 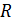 = 290 Дж/(кг×К),
= 290 Дж/(кг×К),
w = 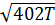 , или wзв = 20
, или wзв = 20 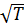 (8,15¢¢)
(8,15¢¢)
Эти формулы показывают, что скорость звука является функцией температуры газа Т, и так как она через коэффициент объемного расширения 1/Т характеризует сжимаемость газа, то, следовательно, и скорость звука является некоторой характеристикой сжимаемости газа. Она показывает, как велико изменение плотности газа при изменении давления. Подставляя kpv = 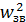 в формулу (8.14), получим
в формулу (8.14), получим

Прежде чем перейти к анализу этого уравнения для случаев соплового и диффузорного движения газов, покажем, что критическая скорость wKP представляет собой скорость распространения звука в данной среде при давлении ру = р2кр и vу = v2кр, так называемую местную скорость звука.
Поскольку процесс истечения принят адиабатным, параметры газа при входе в сопло р1 и v1 и в устье сопла, если в нем есть р2кр и v 2кр, связаны уравнением
p1 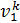 = р2кр
= р2кр 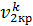 , откуда
, откуда
p1 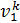 = р2кр
= р2кр 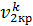 , откуда
, откуда
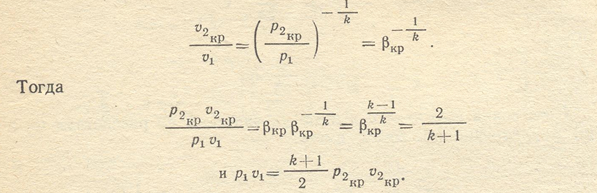
Подставляя полученное значение р1v1 в уравнение (8.12), имеем
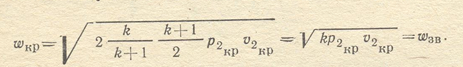
Следует иметь в виду, что если скорость звука равна 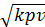 , то, вообще говоря, каждому сечению сопла соответствует своя скорость звука, определяемая величинами р и v в данном сечении.
, то, вообще говоря, каждому сечению сопла соответствует своя скорость звука, определяемая величинами р и v в данном сечении.
Отношение скорости потока w к местной скорости звука wзв носит название числа Маха, обозначаемого Ма, т. е. Ma = w/w3B. Вводя это понятие в уравнение (8.16), получим
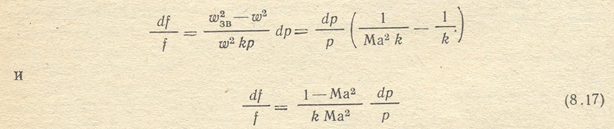
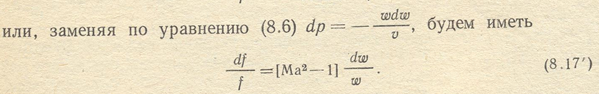
Исследуя на основе полученного уравнения процесс истечения газов через сопла и учитывая, что давление газов при этом понижается, а скорость возрастает, т. е. dp<0, a dw> 0, констатируем, что если dp < 0, то знак df всегда будет противоположен знаку выражения 1– Ма2 тогда:
1) при Ma < 1, (1 – Ма2) >0 (w < wзв - дозвуковая скорость течения), df < 0, т. е. в этом случае сопло является суживающимся;
2) при Ma > 1, (1 — Ма2) < 0 (w > wзв - сверхзвуковая скорость течения) df > 0, т. е. сопло расширяющееся.
Эти выводы показывают, что в суживающихся соплах при звуковой скорости течения газа удельный объем его увеличивается в меньшей степени, чем возрастает скорость, а в расширяющихся соплах при сверхзвуковой скорости течения газов удельный объем их увеличивается в большей степени, чем скорость w.
Здесь же можно показать, что при истечении газов через суживающиеся сопла нельзя получить скорость, которая больше wкр = w3B. В самом деле, если бы в суживающихся соплах можно было достигнуть скорости газов, превышающей скорость звука, тогда в уравнении (8.17) не было бы соблюдено правило знаков, а именно w > w3B, Ма> 1,(1— Ма2)<0 и при df < О имели бы dp>0. Но при dp>0 это
уже не сопло, а диффузор. Следовательно, в суживающихся соплах скорость истечения газов или паров не может быть больше скорости звука и лишь в предельном случае при р = ркр скорость газа на выходе из сопла может равняться скорости звука при параметрах газа в устье, т. е. wKp = wзв. А если это так, значит, давление ру = р2кр = const, несмотря на то что давление среды р2 (куда происходит истечение) будет меньше ру и в пределе теоретически может быть равно нулю.
Для получения скоростей газа, превышающих скорость звука, нужно применить так называемые комбинированные сопла, состоящие из суживающейся, а затем расширяющейся частей (рис. 8.6). В этом случае первая часть сопла будет работать как дозвуковая, а вторая — как сверхзвуковая и в наименьшем сечении этих сопел (горловине) скорость газа будет равна местной скорости звука.
Лекция №6.
Дата добавления: 2021-07-22; просмотров: 674;











