Уравнение первого закона термодинамики для газового потока и понятие об энтальпии газа.
Основные уравнения первого закона термодинамики (2.3) и (2.4) были выведены для процессов, в которых работа расширения газа затрачивалась на преодоление внешних сил и была равна их работе. Изменение кинетической энергии газа при расширении не учитывалось ввиду его незначительности. Такое расширение происходит, например, в поршневых двигателях внутреннего сгорания. В турбинах, реактивных двигателях и других установках, в которых газ перемещается с большой скоростью, пренебрегать изменением кинетической энергии движущихся масс газа нельзя, так как оно является основным слагаемым в энергетическом балансе рабочего тела, и поэтому уравнения первого закона термодинамики (2.3) и (2.4) в этом случае принимают иной вид. Предположим, что по каналу переменного сечения под действием давления движется поток газа (рис. 2.2). При этом будем считать, что:
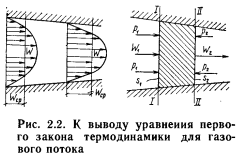
1) движение газа по каналу установившееся и неразрывное. Это означает, что расход массы газа М в единицу времени будет постоянным для любого сечения канала и для любого момента времени:
М = Sw/v = S1 w1/v1 = S2w2/v2 = ... const, (кг/сек)
где S, S1, S2, ..., Sn — площади отдельных поперечных сечений канала; w, w1, w2, …, wn —скорости газа в рассматриваемых поперечных сечениях; v, v1, v2,..., vn – соответствующие удельные объемы газа;
2) скорости по сечению, перпендикулярному оси канала, постоянны. Это допущение равносильно тому, что в каждом сечении берется средняя по расходу скорость;
3) трением частичек газа одна о другую и о стенки канала пренебрегаем;
4) поток газа при своем перемещении технической работы не совершает;
5) изменение параметров от сечения I к сечению II мало по сравнению с абсолютными их значениями.
Очевидно, что количество подводимой теплоты q к 1 кг газа на участке между двумя произвольно выбранными сечениями I—I и II—II будет расходоваться на изменение внутренней энергии  U, на совершение газом работы (называемой здесь работой проталкивания) против внешних сил А' и на приращение кинетической энергии газа (
U, на совершение газом работы (называемой здесь работой проталкивания) против внешних сил А' и на приращение кинетической энергии газа ( 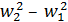 )/2 = А0 , т. е.
)/2 = А0 , т. е.
q =  U+A' + (
U+A' + ( 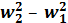 )/2 =
)/2 =  U+A' - А0,(2.6) [3]
U+A' - А0,(2.6) [3]
(А0 = – pdv — в обратимом процессе располагаемая работа (А0 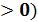 может быть получена лишь при понижении давления в потоке (dp
может быть получена лишь при понижении давления в потоке (dp 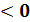 ))
))
а в дифференциальной форме
dq = dU + dA' + 1/2dw2. (2.6') [4]
Уравнения (2.6) [3]и [4](2.6') являются математическим выражением первого закона термодинамики для газового потока.
Для определения работы проталкивания рассмотрим газ, находящийся между сечениями I—I и II—II. На выделенный объем газа действуют массы газов, находящихся слева и справа от сечений I и II. Воздействие этих масс заменяем соответствующими силами, приложенными в указанных сечениях. В сечении I— I будет действовать сила p1S1, а работа, совершаемая в единицу времени этой силой, составит p1S1 l1. Поскольку работа производится внешними по отношению к выделенному объему газа силами, то, согласно принятым обозначениям, ее нужно считать отрицательной. В свою очередь выделенный объем газа сам совершит положительную работу по проталкиванию лежащих впереди слоев в сечении II— II, равную p2S2l2. Тогда, принимая во внимание знаки работ, работу проталкивания при перемещении 1 кг газа можно определить по уравнению А' = p2S2l2 – p1S1l1, где l2 и l1 — пути, пройденные сечениями II и I в 1 с; S2l2 и S1l1 — секундные объемы 1 кг газа v2 и v1. (S2l2 = v2)
Тогда
A' = p2v2 – p1v1 (A' — работа проталкивания) (2.7) [5]
или
A' = R(T2 – T1). (2.7') [5¢]
Из уравнений (2.7) [5] и (2.7') [5¢] следует, что работа проталкивания 1 кг газа представляет собой функцию только состояния газа, так как она нe зависит от направления процесса и зависит лишь от начального и конечного состояний газа.
Подставляя выражение для А' из уравнения (2.7) [5] в уравнение (2.6) [3], получим
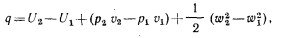
или
q = (U2 + p2v2) – (U1 + p1v1) + ( 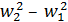 )/2 (2.8) [6]
)/2 (2.8) [6]
Выражение U + pv, входящее в это уравнение, является параметром состояния газа, поскольку U и pv для каждого состояния газа имеют вполне определенные значения. Сумму U + pv называют энтальпией газа и обозначают буквой i. Энтальпия i, так же как и U измеряется в Дж/кг. Тогда, уравнение [6] (2.8) примет вид:
q = i2 – i1 + ( 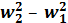 )/2 = i2 – i1 + А0 (А0 – располагаемая работа) (2.8') [6']
)/2 = i2 – i1 + А0 (А0 – располагаемая работа) (2.8') [6']
а в дифференциальной форме
dq = di + wdw. (2.9) [7]
Уравнения (2.8) [6]и (2.9) [7]
наряду с уравнениями (2.6) [3] и (2.6') [4] также являются аналитическими выражениями первого закона термодинамики в применении к газовому потоку и показывают, что теплота, сообщаемая движущемуся газу, расходуется на увеличение его энтальпии и внешней кинетической энергии.
В общем случае поток газа при своем перемещении может совершать и другие виды работ (например, вращать колесо турбины), которые называются техническими и обозначаются Атехн.
Техническая работа может не только отбираться от потока, но и подводиться к потоку (например, поток может нагнетаться центробежным вентилятором). Составной частью работы потока является также работа по преодолению сил трения на стенках канала Атр. С учетом этого уравнение [7] (2.9) примет вид:
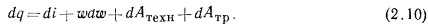 [8]
[8]
По своему существу уравнения (2.4) [2] и (2.10) [8] идентичны — они выражают первый закон термодинамики. Приравнивая правые части этих уравнений, получим
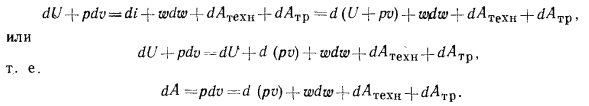
[9]
Таким образом, за счет работы расширения газа, движущегося в потоке pdv, осуществляются работы, расходуемые на проталкивание потока d(pv), изменение кинетической энергии потока wdw, техническая работа dAтехн и работа по преодолению сил трения dAтр.
Если поток газа не совершает технической работы (dAтехн = 0), то
wdw = – vdp — dAтр.
Для течения потока газа без трения wdw = — vdp это важное соотношение используется при рассмотрении процессов истечения газа (см. §8.1).
Следует отметить, что введение понятия «энтальпия газа» в значительной мере упрощает расчеты многих термодинамических процессов, вид и структуру некоторых формул и позволяет использовать графический метод исследования процессов, что исключительно широко применяется, особенно при расчете процессов изменения состояния водяного пара. Как параметр состояния газа энтальпия является функцией любых независимых переменных (р, v, Т), определяющих его состояние, т. е.:
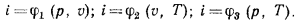
Дата добавления: 2021-07-22; просмотров: 520;











