Представление функций в ЭВМ.

Пусть 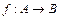, множество А конечно и не очень велико, |A|=n .Наиболее общим представлением такой функции является массив array[А] ofB , где А- тип данных , значения которого представляют элементы множества В . Если среда программирования допускает массивы только с натуральными индексами , то элементы множества А нумеруются ( то есть 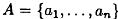) и функция представляется с помощью массива array[1…n] ofB. Функция нескольких аргументов представляется многомерным массивом.

Отступление.

Представление функции с помощью массива является эффективным по времени, поскольку реализация массивов в большинстве случаев обеспечивает получение значения за постоянное время , не зависящее от размера массива и значения индекса.

Операции

Операцией называют функцию, все аргументы и значения которой принадлежат одному и тому же множеству. В общем случае n-местная функция типа φ:М×М×... ×М →М (иное обозначение φ: Мⁿ → М) называется n-арной операцией на множестве М. В таких случаях говорят, что множество М замкнуто относительно операции φ (резуль­тат выполнения операции φ на М принадлежит М).

В частности:

1. Функция одного аргумента φ(x) = у, имеющая тип φ: М→ М, называется унарной операцией. Примеры унарных операций:

· элементаные функции е^х, log x, sin x и др.;

· операция над множествами - дополнение Ā ;

· отображения типа А → А, такие как преобразования, перестановки;

· операции над отношениями: дополнение 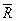, обратное отношение R‾¹, составное отношение R² = R° R, транзитивное R° и рефлексивное R* замыкания и др.

2. Функция двух аргументов φ(x, у) = z, имеющая тип φ: М × М → М, называется бинарной операцией. Примеры бинарных операций:

• арифметические операции: сложение, вычитание, умножение, деление, возведение в степень;

• операции над множествами: пересечение Ç, объединениеÈ, разность \;

• операция композиции функций, отображений, отношений и др. Если над элементами a,b 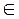M выполняется операция φ, дающая результат z 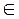M, то это записывается часто как а φ b = z.

Свойства бинарных операций:

1) φ - ассоциативна, если для любых а, b, с из М

(аφb)φс=аφ(bφс)

(арифметические операции сложения и умножения, опера­ции пересечения и объединения множеств, композиция ото­бражений - ассоциативные операции).

Выполнение этого условия (свойства ассоциативности) означает, что скобки в выражении а φ b φ с можно не расставлять;

2) φ - коммутативна, если для любых а, b, с

a φb=b φ а

(арифметические операции сложения и умножения, опера­ции пересечения и объединения множеств - коммутативные операции; арифметические операции вычитания и деления, операция разности множеств, композиция перестановок и преобразований типа А ® А конечного множества - некоммутативны);

3) φ - дистрибутивна слева относительно операции ψ, если для любых а, b, с

a φ (b ψ c) = (а φ b) ψ (a φ с)

и φ дистрибутивна справа относительно операции ψ, если для любых а, b, с

(а ψ b) φ c = (а φ с) ψ (b φ с)

(арифметические операции умножения и деления дистрибутивны относительно операций сложения и вычитания слева и справа, но не наоборот: операции сложения и вычитания недистрибутивны относительно операции умножения и деления; операции объединения и пересечения множеств ди­стрибутивны относительно друг друга слева и справа).