Рефлексивное замыкание отношений

Пусть тождественное отношение Е состоит из упорядоченных пар самого себя – 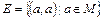. Тогда R*=R°ÈE (R* – рефлексивное замыкание, а R° – транзитивное замыкание).

Если R транзитивно и рефлексивно, то R*=R.

Пример. Используя R – отношение на N такое, что 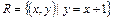получим .

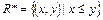Алгоритм Уоршалла.

Вход: отношение, заданное матрицей R.

Выход: транзитивное замыкание отношения, заданное матрицей Т.

S := R

forifrom1tondo

forjfrom1tondo

forkfrom1tondo

T[j, k] := S[j, k] V S[j, i] & S[i, k]

End for

End for

S := T

End for

Заметим, что нас не интересует число путей любой конкретной длины из вершины v_i в вершину v_j. Эта информация, получаемая в процессе вычисления степеней A, далее игнорируется. Для того, чтобы сократить объем вычислений, можно отказаться от получения указанной информации и использовать в вычислениях просто реализуемые булевские матричные операции, которые мы определим согласно.

Обозначим булевскую сумму C двух матриц A и B размера n*n как С=АÈВ, а булевское произведение – D=AÇB.

Элементы матриц C и D задаются соотношениями

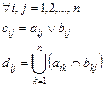
Заметим, что элемент d_ij легко получается путем просмотра i-й строки матрицы A слева направо и одновременно j-го столбца матрицы B сверху вниз. Если k-й элемент в строке матрицы A и k-й элемент в столбце матрицы B равны 1 для какого-нибудь k, то d_ij=1. В противном случае d_ij=0.

Булевы матрицы более экономичны в вычислительном отношении, чем целочисленные. Действительно, запоминание булевой матрицы требует меньшего объема оперативной памяти ЭВМ по сравнению с целочисленной матрицей той же размерности. Кроме того, выполнение на компьютере логических операций над булевыми матрицами требует меньшего объема вычислений, чем над целочисленными матрицами тех же размерностей.

Матрица смежностей, так же как и путевая матрица, является булевской матрицей. Заметим, что .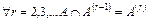

Единственная разница между A² и A⁽²⁾ заключается в том, что A⁽²⁾ является булевской матрицей и элемент на пересечении i-й строки и j-го столбца A⁽²⁾ равен 1 в том случае, когда существует по крайней мере один путь длины 2 из v_i в v_j. Аналогичное положение имеет место для A³ и A⁽³⁾ и в общем случае для A^r и A^(r) при любом целом положительном r. Из этих рассуждений ясно, что матрица достижимости P задается выражением

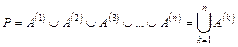
Например, если

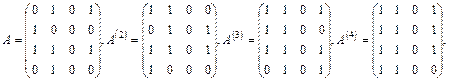то

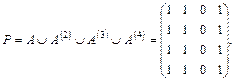
Данный метод получения матрицы достижимости ориентированного графа называется алгоритмом Уоршалла (Warshall S.A. A Theorem on Boolean Matrices. - J.ACM, 1962, 9, pp.11-12).

Тема 5. Функции и отображения. Инъекция, сюръекция, биекция. Представление функций в ЭВМ. Операции. Свойства бинарных операций: ассоциативность, коммутативность, дистрибутивность слева и справа. Способы задания операций. Таблица Кэли.