Прямозубая передача

Приняты следующие допущения:

1. Нагрузка передается одной парой зубьев (l_Σ = b_w) и приложена к вершине зуба по линии зацепления N₁N₂ под углом γ (γ > α_tw) (рис. 4.9).

2. Зуб рассматривается как вписанная в него консольная балка АВС параболического профиля, имеющая равное сопротивление изгибу в сечениях по высоте h_p.

Удельная линейная расчетная нагрузка w_Fn = F_n / l_Σ = F_tK_F / (b_wcosα), где K_F – коэффициент нагрузки при расчете на изгиб (K_F = K_АK_FβK_FvK_Fα). Нагрузка F_tK_F / b_w = w_Ft – удельная окружная и w_Fn = w_Ft / cosα. Нагрузка w_Fn переносится в точку А и раскладывается на составляющие w_Fncosγ и w_Fnsinγ.

В заделке ВС балки возникают напряжения изгиба σ_и = w_Fncosγ∙h_p / W и

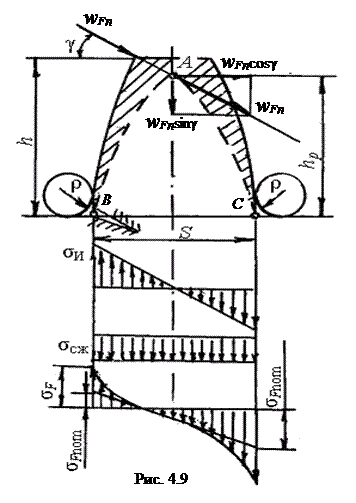сжатия σ_сж = w_Fnsinγ / A, где W – момент сопротивления изгибу сечения ВС; А – площадь сечения ВС при его ширине, равной единице (b_w = 1 мм так как нагрузка w_Fn единичная) и длине s; W = 1∙s² / 6 и А = 1∙s.

Раскрывая последнюю формулу в точке В, будем иметь

σ_F = .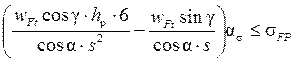

Исходя из геометрического подобия зубьев разных модулей, плечо h_p и толщину s выражают через модуль m: h_p = μm, s = λm, где μ и λ – коэффициенты, учитывающие форму зуба.

Тогда σ_F = .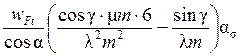

Введя Y_FS = 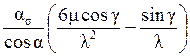– коэффициент, учитывающий форму зуба и концентрацию напряжений, получим

σ_F = w_FtY_FS / m ≤ σ_FP. (4.8) Величины Y_FS приведены в литературе в виде графиков или таблиц.

Подставляя значение w_Ft в формулу (4.8), получим формулу для проверочного расчета прямых зубьев на сопротивление усталости при изгибе:

σ_F = F_tK_FY_FS / (b_wm) ≤ σ_FP. (4.9)

Косозубая передача

Специфика косозубой передачи определяет следующие дополнительные отличия:

1. Наклон контактных линий к основанию зуба учитывается коэффициентом: Y_β = 1 – ε_ββ⁰ / 120 ≥ 0,7,

где ε_β – коэффициент осевого перекрытия зубьев.

2. Лучшая прирабатываемость и большее перекрытие зубьев – Y_ε = 1 / ε_α.

3. Коэффициент Y_FS определяют в зависимости от эквивалентного числа

зубьев z_v = z / cos³β.

Расчетная формула (4.9) для косозубых передач примет вид:

σ_F = F_tK_FY_FSY_βY_ε / (b_wm) ≤ σ_FP. (4.10)