Главная передача (ГП)

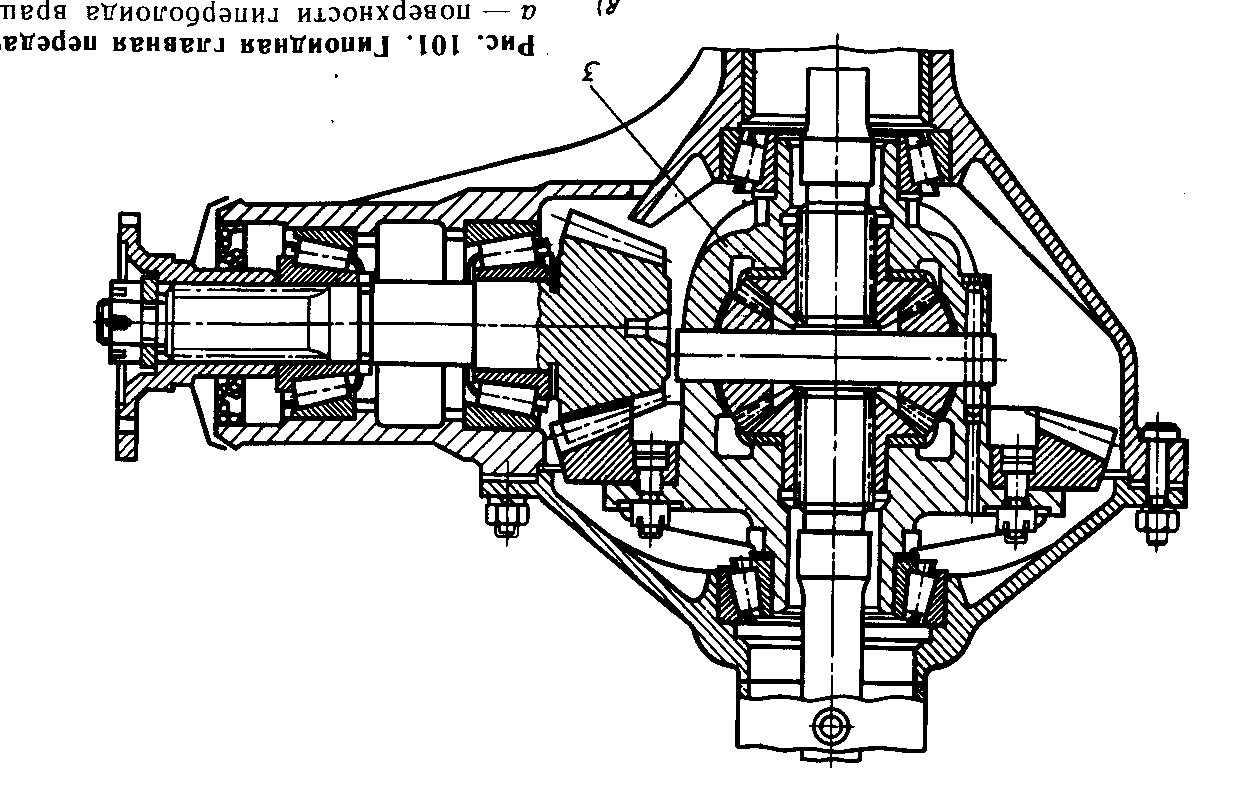
Главная передача служит для увеличения крутящего момента и передачи его под определенным фиксированным углом через дифференциал на ведущие колеса.

Чертеж ГП показан на верхнем, а схема на нижнем рисунке:

Схема ГП показана на рисунке:

Дифференциал

Ведущие колеса

Полуоси

Ведущая шестерня ГП

Ведомая шестерня ГП

Хвостовик ведущей шестерни

ГП представляет собой в простом случае пару конических шестерен. Чем больше передаточное число ГП (u₀), тем меньших размеров получается коробка передач и наоборот. Поскольку, чем меньше от общего передаточного числа приходится на данный узел (КП или ГП), тем меньше в нем диаметры ведомых шестерен, определяющих размер узла. Общее передаточное число трансмиссии ( 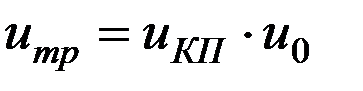), обеспечивающее движение в различных дорожных условиях и режимах находится в диапазоне от 12 у легковых автомобилей до 50 у дорожных грузовых.

Классификация ГП

1. По числу пар зацепления.

1) Одинарная ГП (рассмотренная выше, характерна для легковых и легких грузовых автомобилей).

1 2

3 4

5 4

2) Двойная ГП ( у средних и тяжелых грузовых автомобилей):

1 – ведущая коническая шестерня первой пары шестерен,

2 – ведомая,

3 – ведущая цилиндрическая шестерня второй пары зацепления,

4 – ведомая,

5 – дифференциал.

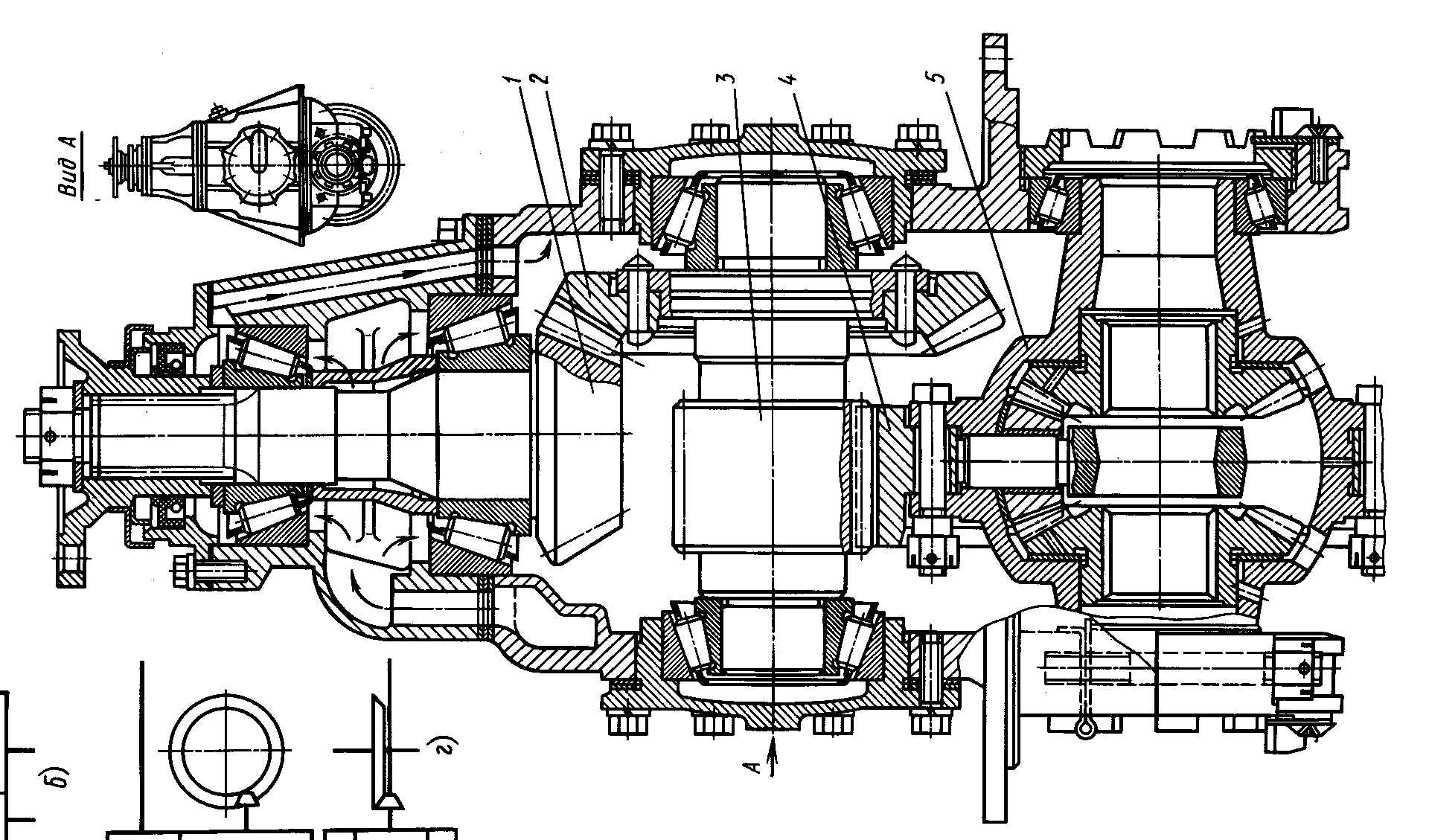
2. По расположению в трансмиссии двойные делятся на:

1) Центральные (показана на рисунке выше).

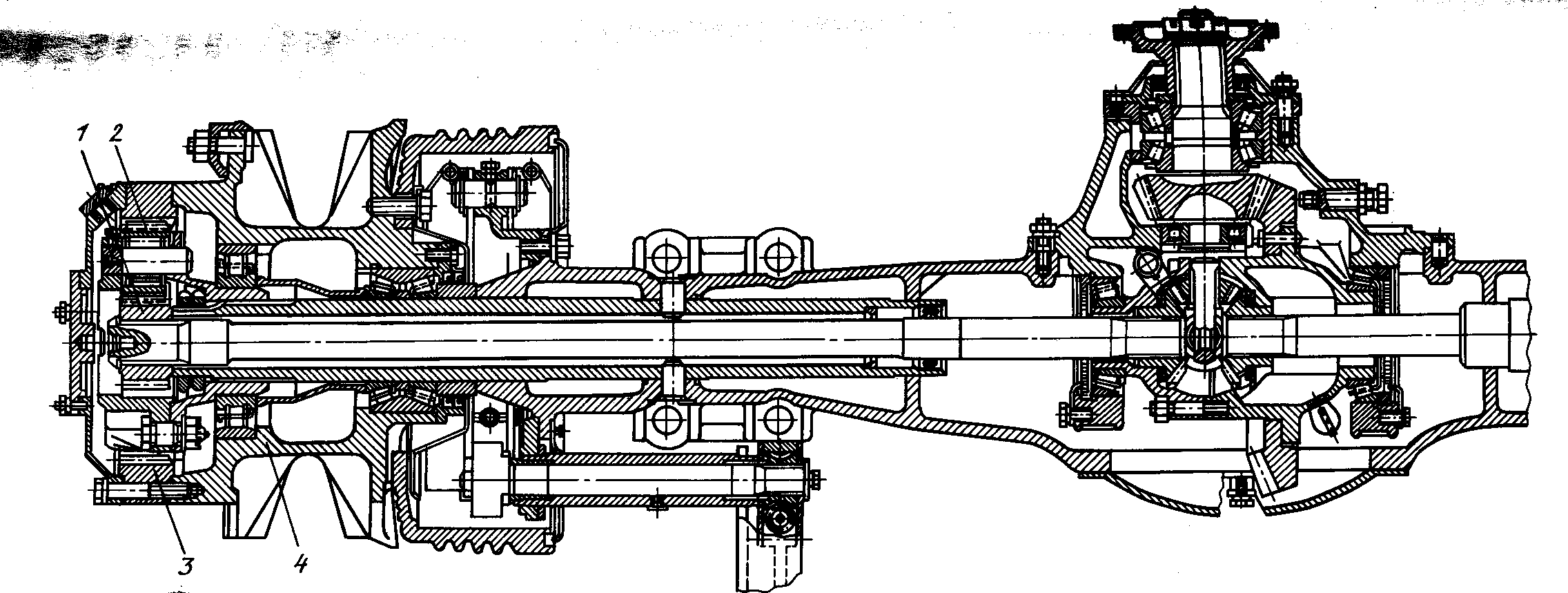
2) Разнесенные. У разнесенных цилиндрическая пара зацепления уносится в колеса в виде колесного редуктора (шестерни размещаются внутри колеса):

1 – планетарный редуктор в ступице колеса,

2 – ступица колеса.

Двойная разнесенная ГП может быть и с бортовым редуктором (пара зацепления размещается перед колесом).

Двойная центральная ГП может быть с переменными передаточными числами (двухступенчатая ГП), как у коробки передач.

3. По виду шестерен одинарные ГП делятся на:

1) Червячные.

2) Конические.

3) Гипоидные.

4) Цилиндрические (у переднеприводных с поперечным расположением двигателя).

1)

2)

3)

е

4. По форме зубчатого зацепления бывают:

1) Прямозубые (сейчас практически не применяются).

2) Косозубые.

3) Шевронные.

4) С винтовым зубом.

Применение двойных разнесенных ГП позволяет существенно увеличить дорожный просвет и разгрузить детали трансмиссии от центрального редуктора до ведущих колес в 3…6 раз. Применяются такие передачи в автомобилях МАЗ, Икарус, троллейбусах и т.д.

Двойные двухступенчатые ГП обычно применяют для автомобилей, работающих на пересеченной местности:

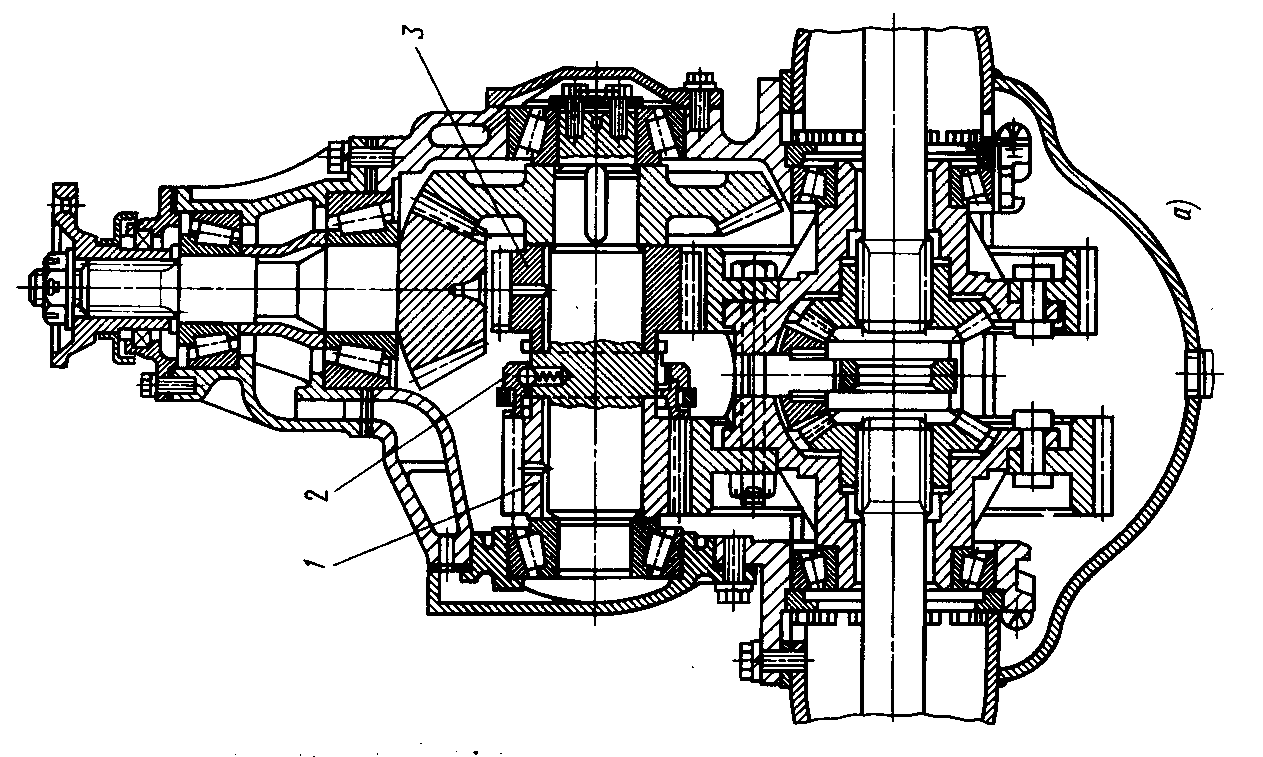
1 – цилиндрическая шестерня пониженной передачи.

2 – муфта переключения передач,

3 – цилиндрическая шестерня повышенной передачи.

Такая передача позволяет существенно расширить передаточный ряд и сохранить стандартные узлы трансмиссии, заменив лишь задний ведущий мост. К недостаткам можно отнести более высокую стоимость и больший вес неподрессоренных масс.

В последнее время простые конические передачи вытесняются гипоидными, которые имеют многие преимущества червячных передач:

- повышенная плавность зацепления и бесшумность работы;

- повышенная нагрузочная способность при тех же габаритах;

- обеспечивает компоновочные преимущества за счет смещения ве- дущего вала вверх у грузовых и вниз у легковых автомобилей.

Недостатком гипоидных передач является более низкий КПД, тем ниже, чем больше смещение е (см. рис.).

Основы расчета ГП

Поскольку большинство конических пар рассчитываются по среднему радиусу зацепления, их расчет можно производить по методике цилиндрических пар путем замены реальной конической на эквивалентную цилиндрическую. Замена производится путем поворота ведомой и ведущей шестерен вокруг полюса зацепления Р в одну плоскость с сохранением величин средних радиусов и ширины "в".

в

Р

Rср

rср

Rср

rср

в

Р

Конические пары требуют очень тщательной регулировки с точностью совпадения вершин образующих конусов до сотых долей миллиметра. Только в этом случае достигается максимальная площадь контакта:

При малейшем изменении регулировки площадь контакта резко снижается:

Линейный Гуляющий контакт

(обратный эллипс)

Подшипники устанавливаются с преднатягом. Взаимное положение шестерен выверяется индикаторной головкой (сначала устанавливается ведущая шестерня, а вместо ведомой вал-приспособление с индикаторной головкой, потом ставится ведомая шестерня относительно ведущей).

Качество регулировки проверяется на краску (тонким слоем красятся зубья ведущей шестерни, прокатываются по ведомой и визуально оценивается площадь отпечатанного контакта).

Признаками разрегулировки являются шум и масло на гайке хвостовика.

Дифференциал, принцип работы, блокировка

Дифференциал служит для распределения потока мощности между ведущими мостами или колесами в определенной пропорции, обеспечивая независимое вращение ведомых звеньев с различными угловыми скоростями (на повороте, по неровной дороге, при различном давлении воздуха в шинах или разном износе протектора, разной степени загрузки ведущих колес и т.д.)

Корпус

Полуосевые шестерни

Палец

Сателлит

ω

Р = 0

Момент от ведомой шестерни ГП передается жестко закрепленному с ней корпусу дифференциала. От него момент переходит на встроенный в корпус палец сателлита. С пальца – на сателлит, который может свободно вращаться на пальце. Сателлит представляет собой шестерню (коническую в данном случае) и находится в зацеплении одновременно с двумя полуосевыми шестернями, на зубья которых передает силу от пальца.

Поскольку сателлит может свободно вращаться на пальце (см. правую часть рисунка), то сила его давления на одну полуосевую шестерню не может отличаться от силы на другую. Именно поэтому моменты на обоих колесах будут равны, независимо от угловых скоростей колес (разные угловые скорости колес легко обеспечиваются сателлитом его вращением вокруг своей оси).

Отмеченное положительное свойство дифференциала в определенных дорожных условиях вызывает большие проблемы. Например: если одно колесо (предположим верхнее на рисунке) находится в воздухе и поворачивается свободно, то к нему нельзя приложить усилие со стороны сателлита (оно не оказывает реакции). Сателлит, легко вращаясь на пальце обкатывает полуосевую шестерню другого, стоящего на земле колеса, и не может нагрузить ее. В таком случае на обоих колесах из-за дифференциала сила тяги будет равна нулю.

Подобный эффект произойдет, если одно из колес находится на поверхности с низким сцеплением (грязь или лед). Другому колесу, стоящему на асфальте сателлит дифференциала будет сообщать точно такой же момент, как первому, т.к. силы по обе стороны сателлита могут быть только одинаковы.

Таким образом, общая сила тяги ведущих колес при работающем симметричном дифференциале определяется колесом, находящимся в худших условиях сцепления с дорогой.

Если сателлиту не позволить вращаться на пальце вокруг своей оси (заблокировать), то он сможет передавать усилие даже одной своей стороной на одно ведущее колесо (например, когда другое колесо повисло в воздухе). В этом случае заблокированного дифференциала кинематические и силовые взаимодействия будут, как если правое и левое ведущие колеса соединены одной жесткой осью. Проходимость автомобиля значительно повышается из-за полного использования сцепления с дорогой каждым ведущим колесом независимо от другого.

Принудительно заблокировать дифференциал (исключить возможность проворота сателлита) можно, используя, например такую конструкцию:

Блокирующая муфта

Привод включения муфты

Зубчатые венцы

ω

Р >> 0

В этой конструкции блокирующая муфта установлена на полуоси с помощью шлицев. Она имеет зубчатый венец, которым может соединиться с зубчатым венцом, закрепленным на ведомой шестерни ГП. При зацеплении зубчатых венцов с помощью привода исключается возможность вращения сателлита вокруг своей оси (см. рисунок справа снизу и сверху) – принудительное блокирование дифференциала.

Существуют принципиально другие конструкции, повышающие проходимость автомобиля. В них провороту сателлита на пальце препятствует трение. Такой дифференциал называются дифференциалом повышенного трения (самоблокирующийся). Пока трение не позволяет провернуться сателлиту, дифференциал вообще заблокирован, как в предыдущем случае. Например, если одно колесо в воздухе, то сателлит давит на полуосевую шестерню другого колеса силой трения, мешающей ему проворачиваться на пальце. Момент трения продолжает действовать и далее, после того, как сателлит начал вращаться вокруг пальца. Момент трения всегда передается сателлитом отстающему колесу (стоящему неподвижно или вращающемуся медленнее другого, забегающего), потому что именно надавливая на его полуосевую шестерню сателлит преодолевает трение, начиная проворачиваться. По этой причине, в случае буксования одного колеса на другое (отстающее) идет момент больший, чем на буксующее (забегающее) на величину момента трения в дифференциале.

Конструктивно получить трение, мешающее повороту сателлита вокруг пальца можно, например, так:

Корпус дифференциала

Фрикционные прокладки

ω

МТ

Р > 0

В обычных дифференциалах (не повышенного трения) также имеется некоторый момент трения, обусловленный касанием сателлита и полуосевых шестерен корпуса дифференциала.

Все выше сказанное относится и к межосевому дифференциалу с той разницей, что вместо ведущих колес у него ведущие мосты.

Классификация дифференциала

1. По расположению в трансмиссии.

1) Межколесные (рассмотрен выше).

2) Межосевой:

2. По кинематике.

1) Симметричный (рассмотрены выше).

2) Несимметричный:

Этот дифференциал вперед отправляет одну часть момента, а назад – две, соответственно количеству ведущих мостов.

3. По способу распределения момента между ведомыми звеньями.

1) Неблокируемые.

2) Самоблокирующиеся (повышенного трения).

3) С принудительной блокировкой.

4.По конструкции.

1) Шестеренчатые конические (из набора конических шестерен, как показано выше на схемах и чертежах).

2) Шестеренчатые цилиндрические (на рисунке – межосевой):

Ведомая шестерня раздаточной коробки

Сателлит

К переднему мосту

К задним двум мостам

3) Червячные.

4) Кулачковые.

5) С муфтами свободного хода.

Кинематические и силовые аспекты работы дифференциала

ωзаб, Мзаб

ωд, Мд

ωот, Мот

В общем случае движения по множеству причин одно из колес имеет угловую скорость отличную от другого. Допустим, сейчас, нижнее на рисунке колесо – отстающее (либо вращается медленнее другого, либо стоит на месте), а верхнее – забегающее.

Для симметричного дифференциала зависимость, связывающая угловые скорости колес ω_от, ω_заб и корпуса дифференциала ω_д выглядит так:

(ω_от + ω_заб) / 2 = ω_д

А в идеальном случае, когда скорости колес равны, они вращаются со скоростью корпуса дифференциала:

ω_от = ω_заб = ω_д.

Момент с корпуса дифференциала распределяется по колесам так:

М_от + М_заб = М_д.

В то же время, о чем говорилось выше, на отстающее колесо действует такой же момент, как на забегающее и еще добавляется момент трения в дифференциале - М_т:

М_от = М_заб + М_т.

В идеальном случае момент распределяется между колесами поровну.

Величина момента трения в дифференциале говорит о степени его заблокированности. Определяется эта величина коэффициентом блокировки:

К_б = М_от / М_заб.

Поскольку по условиям сцепления: М_от = Р_{К от}∙ r_К = φ_от∙ G_K∙ r_К,

М_заб = Р_{К заб}∙ r_К = φ_заб∙ G_K∙ r_К , то получим выражение для коэффициента блокировки:

К_б =φ_от /φ_заб. Здесь r_К – радиус качения колеса, G_K – вес, приходящийся на ведущее колесо (принят одинаковым на оба колеса), φ - коэффициент сцепления между колесом и дорогой.

Если под одним колесом асфальт (φ = 0,8), а под другим – лед (φ = 0,1), то коэффициент блокировки потребуется: К_б = 0,8 / 0,1 = 8, чтобы колеса полностью использовали сцепление с дорогой. Применив записанные выше выражения можно определить, какой требуется для такого случая момент трения в дифференциале:

К_б = М_от / М_заб = (М_заб + М_т) / М_заб = 1 + М_т / М_заб =

= 1 + М_т / φ_заб∙ G_K∙ r_К.

Подставив сюда К_б = 8 и φ_заб = 0,1 получим выражение для момента трения: М_т = 0,7∙ G_K∙ r_К. Это очень высокое внутреннее трение и его может обеспечить только дифференциал специальной конструкции (самоблокирующийся), например, червячный.

Несмотря на лучшую проходимость автомобиля с дифференциалом повышенного трения, имеются существенные недостатки:

- из-за потерь на трение падает КПД трансмиссии;

- увеличивается расход топлива;

- ухудшается управляемость и устойчивость автомобиля на твердой дороге;

- увеличивается износ шин.

Обычно у большинства дорожных автомобилей К_б = 2…2,5;

у кулачкового (повышенного трения) – 3…4;

у червячного – 6…12;

у принудительно заблокированного - К_б = ∞.

Основы расчета дифференциала

rср

r1

ωд

РД

РС

Ось сателлитов

l2

l1

d

В этом дифференциале два сателлита расположенных на одной оси.

На каждый сателлит от корпуса дифференциала действует сила:

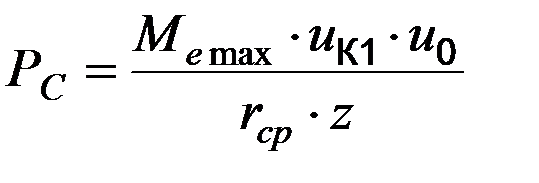, где М_еmax – максимальный момент двигателя, u_К1 – передаточное число КП первой передачи, u₀ – передаточное число главной передачи, r_ср – средний радиус приложения силы к сателлиту, r₁ – радиус приложения силы в корпусе, Z – число сателлитов.

От этой силы ось под сателлитом испытывает напряжение смятия:

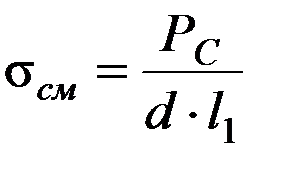, d – диаметр оси, допускаемое напряжение 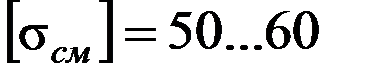МПа.

Напряжение среза пальца по основанию сателлита:

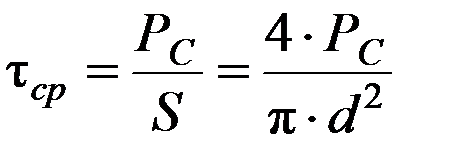, S – площадь среза, допускаемое напряжение 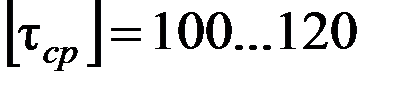МПа.

В корпусе дифференциала на ось действует сила смятия:

.

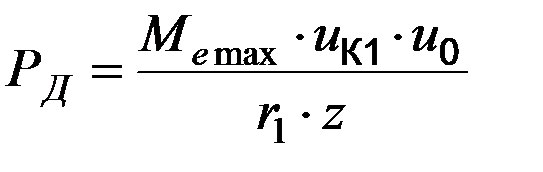Под действием этой силы ось в корпусе испытывает напряжение смятия:

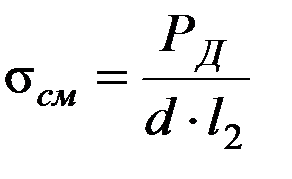, допускаемое напряжение 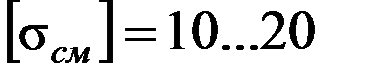МПа.