Расчет на сопротивление контактной усталости

Исходной является формула (4.6), которая в параметрах эквивалентной цилиндрической прямозубой передачи имеет вид:

σ_Н = Z_EZ_HZ_ε[F_tK_H (u_v + 1) / (b_vd_v1u_vU_Н)]^1/2, (4.15)

где U_Н – коэффициент, учитывающий влияние на несущую способность вида конической передачи: для прямых зубьев U_Н = 0,85; для круговых зубьев U_Н является функцией передаточного числа и твердости зубьев (U_Н > 1). Нагрузочная способность передачи с круговыми зубьями в 1,4…1,5 раза выше, чем с прямыми.

Подставив в формулу (4.15) значения параметров, после преобразования получим формулу дляпроверочного расчета стальных конических зубчатых передач на сопротивление контактной усталости при К_be = 0,285:

σ_Н = 6,7∙10⁴[T₂К_Hu / (U _H d_е2³)]^1/2 ≤ σ_HP, (4.16)

где К_Н = K_AK_НβК_НV – коэффициент нагрузки.

По ГОСТ 12289-76 стандартными являются d_е2, и, b.

Поэтому в проектировочном расчете по формуле (4.16) целесообразно определять внешний делительный диаметр колеса

d_е2′ = 1650[T₂К_Hu / (U _Hσ_HP²)]^1/3,

где T₂ , Н∙м; σ_НР , МПа; d_е2′, мм .

Диаметр d_е2′ округляют в большую сторону по ГОСТ 12289-76 (R_a 20).

Расчет на сопротивление усталости при изгибе

Расчет ведут по зубу шестерни.

Исходной является формула (4.9) для эквивалентной прямозубой цилиндрической передачи, которая для зубьев конической передачи будет иметь вид:

σ_F1 = F_t К_FY_FS1 / (bm_nmU_F) ≤ σ_FP1; σ_F2 = σ_F1Y_FS2 / Y_FS1 ≤ σ_FP2, (4.17)

где К_F = K_AK_FβК_FV – коэффициент нагрузки на изгиб; U_F – коэффициент, учитывающий влияние вида конической передачи при изгибе (для прямых зубьев U_F = 0,85); Y_FS – коэффициент формы зуба: определяется по формуле (графикам) для прямозубых цилиндрических передач в зависимости от z_vnm = z / (cosδcos³β_m).

В проектировочном расчете открытыхили закрытых высокотвердых передач (HRC > 56) из условий изгиба (формула (4.17)) определяют модуль:

m_te′ = 14[T₁К_FY_FS1 / (ψ_mU_Fz₁σ_FP1)]^1/3,

где ψ_m = b / m_te – коэффициент ширины венца по внешнему модулю.

Величинами ψ_m и z₁ следует предварительно задаваться. Модуль m_te′ округляют по ГОСТ 9563-60 в большую сторону.

В силовых передачах m_te ≥ 1,5…2 мм.

ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ

Общие сведения

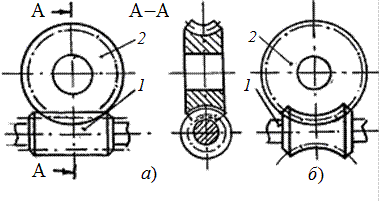
Червяк (z₁)1 (рис. 5.1) – это винт с трапецеидальной или близкой к ней резьбой. Червячное колесо (z₂) 2 – косозубое цилиндрическое колесо с вогнутыми по длине зубьями.

Червячная передача – зубчато-винтовая передача с преобразованием движения по принципу винтовой пары. Направление витков червяка и зубьев колеса одинаковое. Ведущим является червяк. Вращение определяется по типу завинчивания винта и гайки. При этом направление вращения колеса зависит от расположения червяка (верхний, нижний).

Тип передачи определяют по червяку.

В зависимости от формы внешней поверхности червяка передачи бывают

с цилиндрическим 1 (рис. 5.1, а) или глобоидным 1 (рис. 5.1, б) червяком.

Рис. 5.1

На практике в основном применяют передачи с цилиндрическими червяками.

В зависимости от способов нарезания винтовой поверхности червяка различают линейчатые (винтовые поверхности могут быть образованы прямой линией) и нелинейчатые червяки.

Нарезание линейчатых червяков осуществляют прямолинейной кромкой резца на токарно-винторезных станках. Это архимедов(его обозначают ZA), конволютный(ZN) и эвольвентный червяки (ZI).

Нелинейчатые червяки нарезают дисковыми фрезами конусной (червяки

ZK) или тороидальной(червяки ZT) формы. Витки нелинейчатых червяков во всех сечениях имеют криволинейный профиль: в нормальном к витку сечении выпуклый, в осевом сечении - вогнутый.

Для силовых передач следует применять эвольвентные и нелинейчатые

червяки.

В червячных передачах стандартным (ГОСТ 19672-74) является осевой модуль.

На работоспособность червячной передачи сильно влияет жесткость червяка. Для исключения маложестких червяков введен стандартный параметр q – коэффициент диаметра червяка: q = 8; 10; 12,5; 16; 20; 25.

Диаметр делительной окружности, где толщина витка равна ширине впадины, червяка: d₁ = mq.

Число заходов (витков) червяка z₁ = 1, 2 и 4.

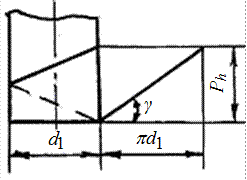
Рис. 5.2

Угол a профиля: для червяков ZA, ZN, ZI a = 20°; для ZT a = 22°. Делительный угол g подъема витка червяка (рис. 5.2): tg g = Ph / (pd1), где Ph = Pz1 – ход витка, Р – шаг червяка; tg g = pmz1 / / (pmq) = z1 / q. Зубья червячных колес нарезают червячными фрезами, которые являются копи- ями червяков с режущими кромками на витках

Рис. 5.3

и имеют больший (на два размера радиального зазора в зацеплении) наружный диаметр. Заготовка колеса и фреза совершают те же движения, какие имеют червячное колесо и червяк при работе. Основные геометрические размеры венца червячного колеса определяют в среднем его сечении (рис.5.3). Во избежание подреза ножки зуба при нарезании число зубьев z2 принимают больше 28; максимально 80. Оптимальным является z2 = 32…71. Диаметр делительной окружности

колеса d₂ = mz₂.

Межосевое расстояние червячной передачи a = 0,5(d₁ + d₂) = 0,5m(q + z₁).

Передаточное число u = z₂ / z_1­­­. Так как z₁ = 1, 2 и 4, z₂ = 28…80, то в одной паре можно получить u = 7…80.

Для сокращения номенклатуры червячных фрез (копии червяков) по ГОСТ 2144 – 93 стандартизованы параметры: u, a_w, m, q, z₁, z₂.

С целью вписания передачи с произвольно заданным передаточным числом u в стандартное межосевое расстояние a_w выполняют смещение (xm) фрезы при нарезании зубьев колеса (рис. 5.3):

a_w = a + xm; a_w = 0,5m(q + z₂ + 2x), (5.1)

отсюда x = (a_w / m) – 0,5(q + z₂).

Если a = a_w, то x = 0 – передача без смещения. Предпочтительны положительные смещения – повышается прочность зубьев колеса.

Рекомендуют для передач с червяками:

1) ZA, ZN, ZI–1 £ x £ + 1 (предпочтительно x = 0,5). Из формулы (5.1) следует, что при a_w = const за счет смещения в пределах x = ± 1 можем иметь z₂ = z_2ГОСТ m 2, т.е. стандартное число зубьев z_2ГОСТ можем изменять в пределах двух зубьев, что позволяет варьировать u = z₂ / z₁, отличая его от стандартного.

2) ZT1,0 £ x £ 1,4 (предпочтительно x = 1,1…1,2).

Силы в зацеплении

В плоскости зацепления b – b (рис. 5.4, а) на витки червяка и зубья колеса действует нормальная сила F_n.

Ее осевую составляющую F_nx1 раскладываем в осевой плоскости x – x (рис. 5.4, б) червяка на осевую F_a1 и радиальную F_r1 силы. Окружная сила F_t1 = = 2000T₁ / d_w1 направлена против вращения n₁ червяка (рис. 5.4, в – на рис. z₁ и z₂ условно разнесены). По отношению к зубу колеса F_t1 = F_a2 является осевой силой. Окружная сила F_t2 = 2000T₂ / d₂ , где T₂ = T₁uh (h – КПД передачи), направлена в сторону вращения n₂ колеса. Для червяка F_t2 = F_a1 является осевой силой, радиальные силы F_r1 = F_r2 = F_t2tga (рис. 5.4, б). Нормальная сила (рис. 5.4, а, б) F_n = F_t2 / (cosacosg_w), где g_w – угол подъема червяка со смещением.