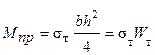По методу допускаемых напряжений предельной нагрузкой является

М_т = 226,5Н·м, и допускаемый крутящий момент:

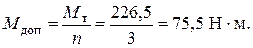
По методу предельного состояния величина допускаемого момента равна

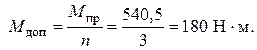
Сравнивая эти допускаемые моменты, заключаем, что расчёт по предельному состоянию вскрывает дополнительные прочностные ре­сурсы по сравнению с методом допускаемых напряжений.

3.Нагружение за пределы упругости и разгрузка.

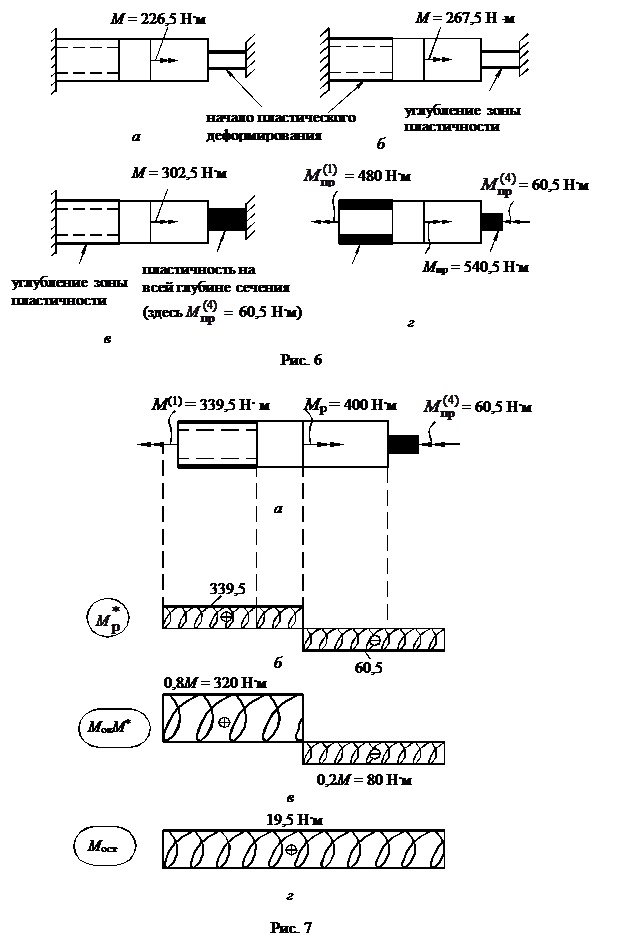
Приложим к валу нагрузку М_р = 400 Н·м. Эта нагрузка выше на­грузки текучести и ниже предельной нагрузки, вызывает текучесть всего сечения четвёртого участка. Поэтому крутящий момент на пер­вом участке можно определить из уравнения равновесия (рис.7,а):

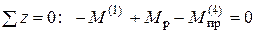; – М⁽¹⁾ + 400 – 60,5 = 0.

Отсюда М⁽¹⁾=339,5 Н·м.

Этот момент больше 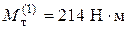и меньше Н·м, по­этому он вызовет упругопластическую деформацию второго участка. Крутящий момент на участке 3 всегда равен крутящему моменту на участке 4. Итак, эпюру внутренних усилий от М = 400 н · м покажем на рис.7,б.

Теперь вал разгрузим, т.е. уберём приложенный момент

М* = 400 Н·м. Известно, что разгрузка происходит по линейному за­кону, поэтому следует от эпюры моментов М_р отнять эпюру крутящих моментов статического расчёта М_ок (рис.2,г), все значения которой умножить на

М* = 400 Н·м (рис.7, в).

В результате вычитания, получим эпюру остаточных крутящих мо­ментов М_ост (рис.7, г), которые вызывают остаточные напряжения в рассмотренном вале.

Таким образом, упругопластический анализ вскрывает дополни­тельные ресурсы прочности вала.

5.4.ИЗГИБ БАЛОК И РАМ

Пример 1. Выполним упругопластический расчёт и исследуем пре­дельное состояние балки на двух опорах (рис. 5.17, а), для которой эпюра изгибающих моментов от силы Р показана на рис. 5.17,6; ус­ловная диаграмма растяжения (рис.5.17,в) принята для идеально упруго пластического без упрочнения.

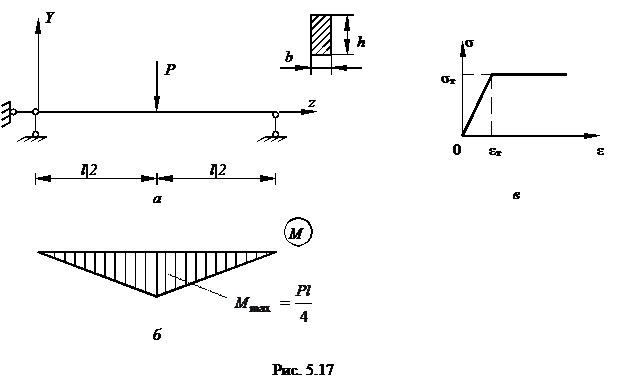
При некотором значении силы Р = Р_т в наиболее напряженном сечении балки возникнут пластические деформации. Это произойдет тог­да, когда наибольшие нормальные напряжения в точках, наиболее удалённых от нейтральной линии, в среднем сечении (z = l/2) достиг­нут величины предела текучести σ_т или, что то же, когда изгибающий момент в среднем сечении сравняется с величиной М_т(М_т =σ_тW_x; . W_x= bh\ 6 – для

прямоугольного сечения).

Для определения Р_т приравняем изгибающие моменты М_мах = М_т.

отсюда

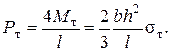
При увеличении силы Р свыше Р_т в балке образуется пластическая область, т.е. область, напряжения в которой равны пределу текуче­сти σ_т.

Rв = Рпр/2

в

l/2

l/2 l/2

Предельное состояние образуется при достижении силой Р предель­ного значения. При этом несущая способность балки исчерпывается полностью (балка становится геометрически изменяемой), т.к. в сред­нем сечении исчезает упругая область (рис.5.18,а). Принято говорить, что в этом сечении балки возникает пластический шарнир. Последнее объясняется тем, что в сечении так называемого пластического шарни­ра изгибающий момент постоянен и становится равным предельному моменту М _пр (рис.5.18,6) и больше увеличиваться не может.

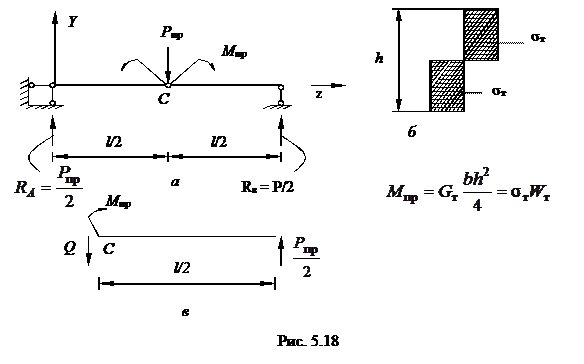Величину предельной силы Р_пр получим, приравнивая изгибающий момент (сверх предельного) в среднем сечении (z = l/2) нулю (рис.5.18, в)

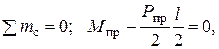
отсюда следует

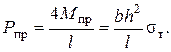
Сравнивая Р_т и Р_пр видим , что

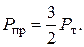
Определим границу упругой и упруго – пластической области. Рассмотрим рис.5.19 на котором показана отсеченная часть балки. Запишем уравнение равновесия 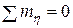элемента балки длиной Z_т относительно точки h (рис.5.19,6), относительно сечения, в котором возникает момент текучести M_т= σ _тW_x:

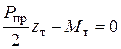
отсюда

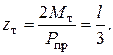
Область, в которой возникла пластичность, изобразим на рис.5.19,в.

В пределах изменения z от 0 до z_т участок балки является упругим, а в пределах от z _т до 1/2 – упруго – пластическим.

Пример 2. Выполним упругопластический анализ балки на двух опорах (рис.5.20,а), имеющей прямоугольное поперечное сечение, от действия равномерно распределённой нагрузки q. Диаграмма растяжения принята для идеально упругопластического материала без упрочнения (рис. 5.20,в).

На рис. 5.20 в изобразим эпюру изгибающих эпюру изгибающих моментов, а на рис.5. 20 г рассмотрим левую отсеченную часть балки, на которую действуют со стороны отброшенной правой части напряжения s.В центре балки в ее крайних волокнах в сечениях Y= ± h / 2 напряжения достигают значений текучести s = s_т при нагрузке q = q_т. Эти напряжения создают изгибающий момент М_т = s_т ×W_x.

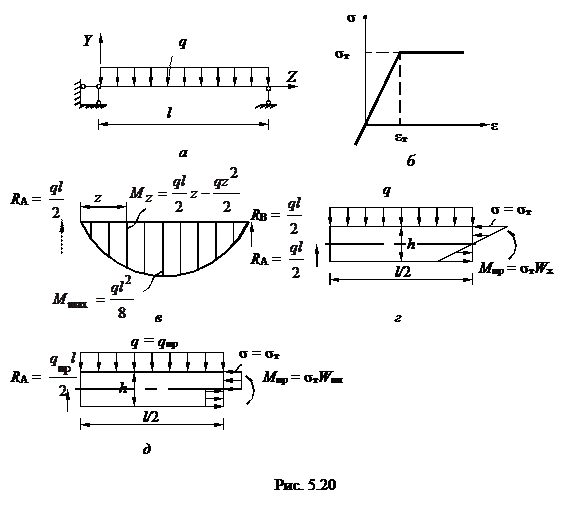
Согласно рис. 5.20 в и рис.5.20 г для определения (нагрузки текучести 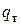нагрузка q при этом становиться нагрузкой текучести q_т) приравниваем моменты :

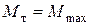G_тW_x =q_т l² /8

из этого равенства нагрузку текучести q_т определим

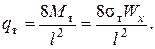
Итак в центре балки Z=l/2 в её крайних волокнах возникли напряжения .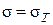

Увеличим нагрузку q до такой величины, когда в центре балки возникнет пластический шарнир нагрузки q g при этом будет называться предельной нагрузкой q_пр. При верхнем пластическом шарнире во всем сечении Z=l/2 возникнут напряжения G_т (рис.5. 20 д)

Для определения предельной нагрузки 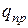согласно рис. 5.20 в и

рис. 5.20 д приравняем моменты :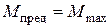

G_тW_x = q_прl²/8

Отсюда определим

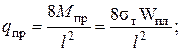
учитывая, что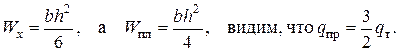

При возникновении пластического шарнира в центре балки зона пластичности будет расширяться при удалении от нейтрального слоя (рис.5.21,а). Границу упруго и упруго - пластического участков опреде­лим, записав уравнение равновесия упругого участка длиной Z_т.Запишем сумму моментов всех сил относительно точки 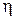(рис.5.21,б):

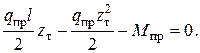
Решение поперечного квадратного уравнение дает

.

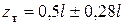Отсюда получим два значения между которыми находится пластическая область:

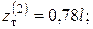
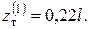
Изобразим область, в которой возникла деформации текучести на

рис.5. 21 в.

	Рис. 5.21

Заметим ,что уравнение равновесия для определения пластической области следовало бы заметить в виде неравенства, 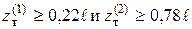чтобы получить

Пример 3. Выполнить расчёт по предельному состоянию статически неопределимой балки (рис.5.22,а) с целью определения предельной нагрузки Р, если 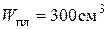, s_т = 20 кН/см², 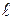= 6 м. (Влияние собственного веса и поперечной силы не учитывать).

Сначала выясним, где может возникнуть пластический шарнир. Для этого построим эпюру изгибающих моментов от нагрузки в статически определимой балке (рис.5.22,б). Пластический шарнир может быть под одной из сил Р₁ или Р₂. Воспользуемся эпюрами (рис.5.22,в), построенными от силы Р как в статически определимой балке (треугольник АСВ) с максимальным моментом 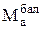и как в балке (эпюра АСВ заштрихована), в которой возникло два пластических шарнира от моментов М_пр. Из геометрических соотношений получаем

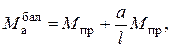
откуда

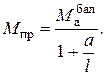
Теперь, если пластический шарнир находится под силой Р₁(а = 2м), то

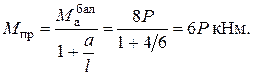
Если пластический шарнир под силой Р₂ (а = 4м), то

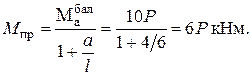
Значения М_пр получились одинаковыми - это значит, что всякое по перечное сечение балки между силами Р₁ и Р₂ будет находится в состоянии пластического шарнира (рис.5.22,г).

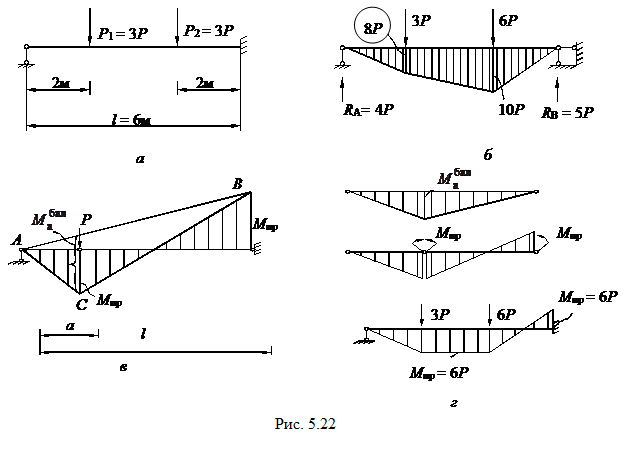
Из условия предельного состояния М_пр = σ_тW_пл или

6Р кНм = 20 кН/см² · 300 см⁴, получим Р = 10 кН.

Пример 4. Определить параметр ц для балки (рис.5.23,а), для которой

W_пл= 300 см³, σ_т =20 кН/см², l = 6 м.

Положение пластического шарнира неизвестно. Для его определения рассмотрим рис.5.23,б, где изображены две эпюры моментов: – от момента в М_пр правом шарнире (линейная зависимость АВ) и от нагрузки q, построенной в статически определимой балке с шарнирами на обоих концах (рис.5.23,в) в виде квадратной параболы. Из рис.5.23,б видим, что на z расстоянии от левой опоры .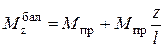

Последнее выражение перепишем так:

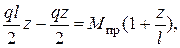
отсюда выразим М_пр:

.

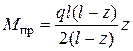Чтобы определить положение пластического шарнира приравняем нулю производную М_пр по координате z :

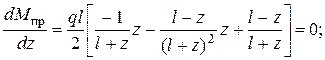
или упростив выражение в квадратных скобках получим уравнение:

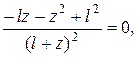
которое, при (l+ z) # 0, приведёт к квадратному уравнению

z² + 2lz – l² = 0.

Его положительный корень z = 0.414l определяет положение пластиче­ского шарнира внутри балки.

Воспользуемся опять выражением 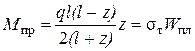из которого определим q при z = 0.414ℓ= 2,484 м:

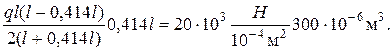
Отсюда следует величина нагрузки q = 19.4 кН/м, при которой в сечении z = 2,484 м возникает пластический шарнир. При­ближенный результат можно получить, если предположить, что пласти­ческий шарнир расположен в точке z = l/2, тогда q = 20 кН/м.

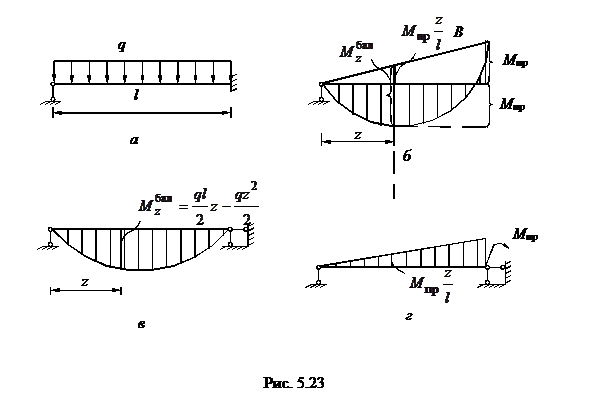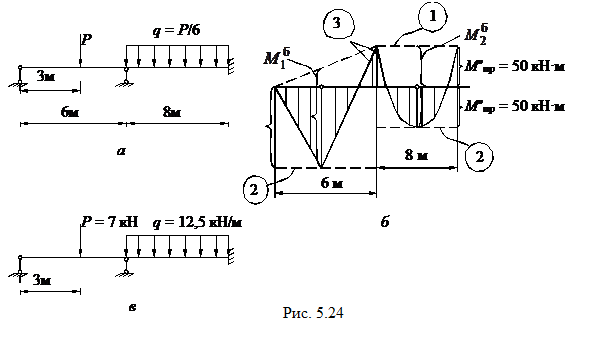
Пример 5. Определить предельную нагрузку для неразрезной балки (рис. 5.24) при совместном действии сосредоточенных сил и равномер­но распределённой нагрузки при условии, что предельные моменты в первом пролёте М_пр = 100 кН ∙ м, а во втором М_пр = 50 кН∙ м (М_пр =σ_тW_т). Опорный момент над средней опорой надо принять меньшим, т.е. 50 кНм. Все необходимые построения показаны на рис.5.24.

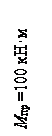Расчёт ведётся следующим образом:

1. Нагрузка по всей балке должна быть выражена одним параметром, который и является искомой величиной (Рис.5.24,а).

2. По наименьшим сечениям из примыкающих к опоре пролетов определяются предельные опорные моменты М_пр= σ_тW_пл. Их значения откладываются сверху от базы эпюры изгибающих моментов, совмещаемой с осью балки, и пунктиром изображаются эпюры изгибающих моментов от этих опорных моментов (линия );

3. В каждом пролете в соответствии с его сечениями определяются предельные моменты М_пр= σ_тW_пл и снизу балки проводится линия штриховая предельных моментов;

4. К линии опорных моментов "подвешивается" эпюра изгибающих моментов простой балки, соответствующая типу нагрузки на данном пролете (линия ), с таким расчётом, чтобы она снизу касалась линии предельных моментов (рис. 5.24,6);

5. Исходя из предположения о разрушении каждого пролета в от­дельности, определяем параметр предельной нагрузки и выбираем наименьшее значение.

Предельная нагрузка в первом пролете:

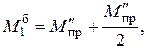
или

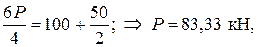
соответственно q = 13,89 кН/м.

Предельная нагрузка во втором пролете:

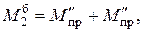
или

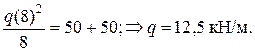
Учитывая, что q = Р/6, последнее равенство можно записать и так:

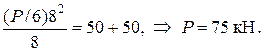
Предельная нагрузка при меньшем значении параметра Р = 75кН; показана на рис.5.24, в.

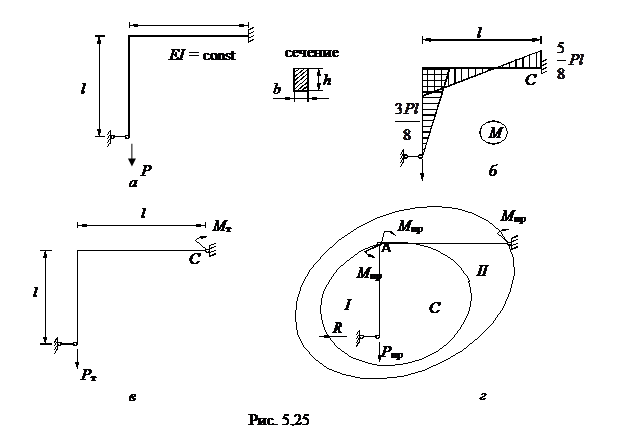
Пример 6. Определить последовательность образования пластических шарниров, нагрузку текучести Р_т и предельную нагрузку Р_пр в статически неопределимой раме постоянной жёсткости Е1 (рис.5.25а).

Чтобы определить "характер" внутренних моментов с целью определения нагрузки текучести Р_т решим статически неопределимую задачу - расчёт рамы методом сил. Результат расчёта изображен на рис.5.25,б. Видим, что пластический шарнир начнет возникать в сечении С. Когда в крайних волокнах сечения в точке С начнут возни­кать напряжения а_т, то в этом сечении "появится" момент М_т =σ _тW_х и он направлен соответственно по часовой стрелке. Следовательно из равенства 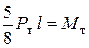можно определить нагрузку текучести.

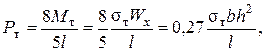
где W_x=bh²/6 – момент сопротивления прямоугольного сечения.

Эпюра М на рис. 5.25,6 даёт характер действия предельных момен­тов М_пр. В узле С рамы раскрываются верхние волокна, а в узле А рас­крываются нижние волокна. Хотя оба момента М_пр в узле А, можно изобразить приложенными наоборот - всё равно решение будет единственным.

Итак, в соответствии с изображёнными предельными моментами (рис.5.25,г) запишем уравнения равновесия:

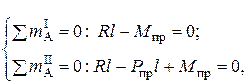
отсюда определим предельную нагрузку 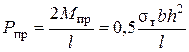.При

этой нагрузке в сечениях А и С образуются пластические шарниры

М_пр = σW_пл, где W_пл = bh²/6 - пластический момент сопротивления прямоугольного сечения.

Пример 7. Для заданной статически неопределимой рамы (рис.5.26,а) постоянной жёсткости и действующей нагрузкой Р и q определить предельную и нагрузку текучести. ×Поперечное сечение рамы

b h= 0,1м · 0,1м.

Будем считать нагружение простым, т.е. нагрузки меняются пропор­ционально одному параметру (рис. 5.26,6). Чтобы решить задачу жела­тельно знать характер возникающих в раме моментов. Для этого решим задачу (рис. 5.26,6) методом сил (см. дополнение). Решение показано на рис.5.27,а.

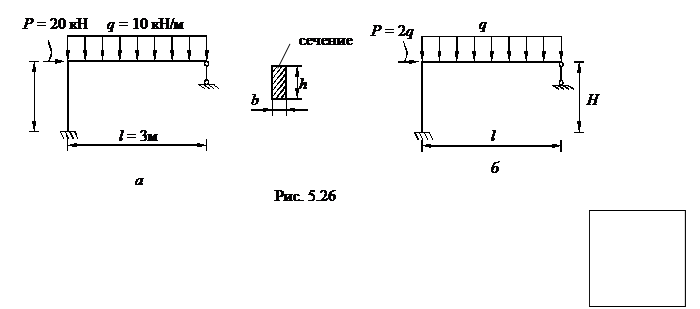Наиболее нагруженным оказывается сечение у левой опоры А –

М_мах = 2,0625q. Приравняв этот момент моменту текучести получим

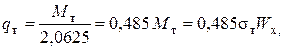
где

W_x=bh²/6.

Подставим значения М_т при σ_т = 200 мПа.

Тогда q_т = 0,485 м^-2 ·200 мПа 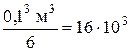кН/м, а сила Р должна быть 32 кН, чтобы возникли напряжения текучести.

Анализируя эпюру 5.27,а видим, что при дальнейшем нагружении рамы пластические шарниры будут образовываться в точках А (опора левая) и С (середина пролета); причем моменты будут раскрывать шарниры так, как показано на рис.5.27,б.

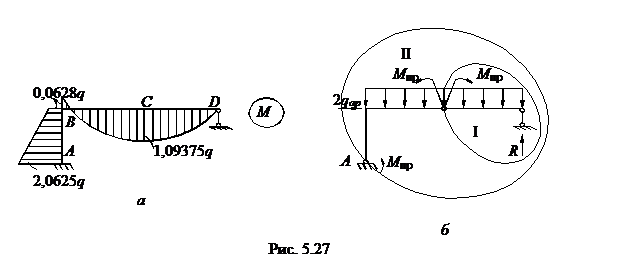При образовании второго пластического шарнира рама превратится в геометрически изменяемую (механизм) - несущая способность её будет исчерпана.

Запишем уравнения равновесия в соответствии с приложенными усилиями на рис.5.27,б:

: ;

:

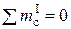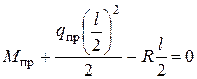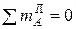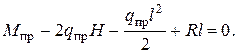
Подставив из первого уравнения во второе R, определим :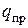

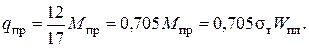
Зная, что W_пл= 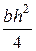, определим значение предельной нагрузки 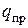для рассматриваемой рамы:

.

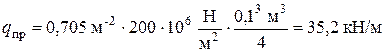Соответственно предельная сила Р должна быть не более 70.4 кН. Таким образом раму можно догружать до Р 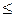70.4 кН, а 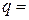35,2.

Но в процессе догружения обе силы Р и q следует изменять только пропорционально.

Дополнение к задаче.

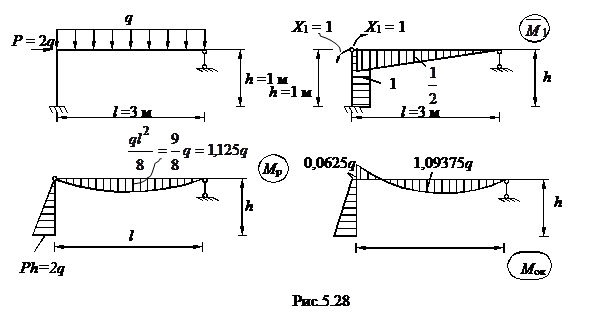Расчет методом сил изображен на рисунке 5.28.

	l

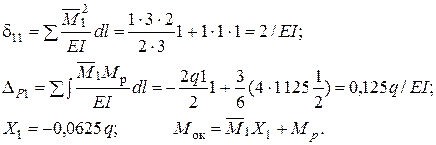
Проверка:

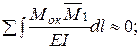
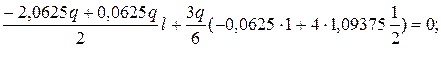
или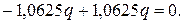

Контрольные вопросы

1. С какой целью выполняются расчеты за пределом упругости?

2. Какое состояние называется предельным?

3. В чем различие понятий: прочность материала и прочность конструкции? В чем измеряется прочность материала и в каких единицах может измеряться прочность конструкции?

4. Что называют «пластическим шарниром»?

5. Какие диаграммы деформирования используются при исследовании предельных состояний?

6. Сравните моменты сопротивления поперечного прямоугольного сечения при упругом деформировании, упруго-пластическом деформировании и пластическом состоянии при возникновении пластического шарнира.

7. Как распределяются нормальные напряжения в балке при упругой работе при возникновении пластического шарнира?

8. Какие нагрузки называют допускаемыми нагрузками? Какие нагрузки называют предельными нагрузками?

9. Объясните термин «несущая способность» балки.

10. В каких волокнах прямоугольного сечения балки начинают возникать пластические деформации?

11. Как вы думаете, почему при пластическом деформировании балки рассматриваются только нормальные напряжения и не учитываются касательные напряжения? Почему не рассматриваются точки в сечении, где совместно действуют нормальные и касательные напряжения?

12. При центральном растяжении стержня квадратного поперечного сечения возникают ли касательные (сдвигающие) напряжения? Если возникают, то как определить их значения?