КРУЧЕНИЕ КРУГЛЫХ ВАЛОВ

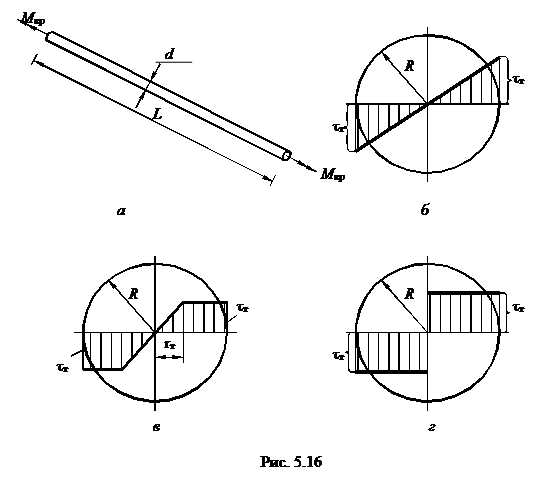
Пример 1 . Рассмотрим задачу о предельном равновесии круглого вала. Требуется определить величину крутящего момента, при котором возникнут пластические деформации и предельный крутящий момент, который может выдержать стальной круглый вал (рис. 5.16,а) диаметром d= 1 см., если τ_Т= 80 мПа, G = 80 ГПа.

Крутящий момент, при котором начнут образовываться касательные напряжения τ_т (напряжения текучести), равен

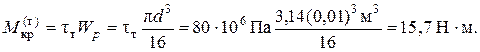
Эпюра касательных напряжений при таком моменте показана на рис.5.16,б.

Крутящий момент, при котором касательные напряжения текучести "проникнут" на расстояние R – r_т вглубь вала (рис.5.16,в), т.е. например при r_т = R/2, имеет величину

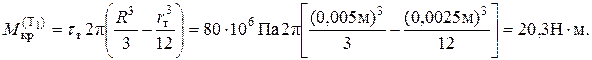
Предельный крутящий момент образуется тогда, когда касательные напряжения текучести проникнут до продольной оси вала при r_т = 0 (рис.5.16,г):

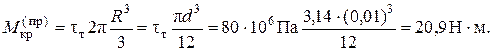
Предельный крутящий момент 20,9 нм больше момента текучести 15,7 нм в 1,33 раза. Момент 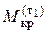отличается от 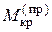на 3 %.

Определим углы закручивания вала длиной L в процессе деформирования.

В упругой стадии, точнее, в начале появления текучести, угол за­кручивания φ равен:

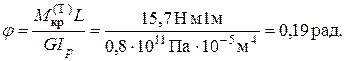
Здесь учтено, что

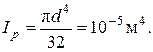
В состоянии, когда текучесть распространится до r_т = R/2 - угол закручивания увеличится

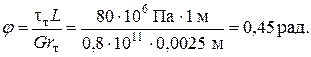
Когда текучесть распространится до оси вала (r_т = 0), тогда φ → ∞ и вал полностью перестанет сопротивляться действующим моментам.

Пример 2. Выполнить упругопластический расчёт круглого вала ступенчато-переменной жёсткости от действия крутящего момента М (рис.1,а). Вал изготовлен из стали 40Х, для которой σ_т = 400 кН/м² ; в левой части вал имеет трубчатое сечение, а по торцам жёстко защемлён.

Определить величину крутящего момента М = М_т, при котором возникнут напряжения текучести τ_т в сечениях вала, предельный крутящий момент М = М_пр для всей конструкции и остаточные усилия, получаемые в результате разгрузки.

По характеру напряжённого состояния выделим в вале четыре участка, номера которых обозначим верхними индексами, заключёнными в круглые скобки. Например, внутренний и внешний диаметры первого участка обозначим как 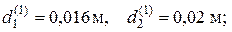диаметры второго и третьего участков – d⁽²⁾ = d⁽³⁾ = 0,02м; соответственно диаметр четвёртого участка

d⁽⁴⁾ = 0,01 м (рис.1,б). Иногда, для удобства, вместо диаметров будем использовать радиусы сечений, соответственно 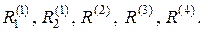Текущий радиус обозначим символом ρ. Введём правило знаков для крутящих моментов, возникающих в вале: поло­жительными будем считать направления внутренних моментов, кото­рые совпадают с направлениями нормалей этих сечений.

1.С т а т и ч е с к и й р а с ч ё т. Закреплённый по торцам вал представляет собой статически неопределимую систему, расчёт которой выполнен методом сил и продемонстрирован на рис.2. Полярные моменты инерции поперечных сечений вала вычислим по известным формулам:

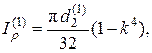
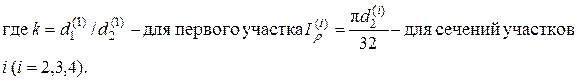
Теперь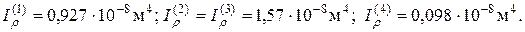

В основной системе метода сил (рис.2 а,б) угол поворота правого торца вала равен сумме углов поворота всех участков

φ = φ⁽¹⁾+ φ⁽²⁾+ φ⁽³⁾+ φ⁽⁴⁾,

где 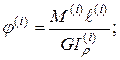l⁽ⁱ⁾ длина участка 1; М⁽ⁱ⁾ - крутящий момент,

действующий на участке i (здесь М⁽ⁱ⁾ = М_А = соnst); G - модуль сдвига

(G = 2 Мн/м²).

Тогда, в соответствии с рис.1, а.

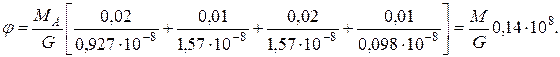Угол поворота правого торца вала от действия внешнего момента М (рис.1,б) определяется аналогично:

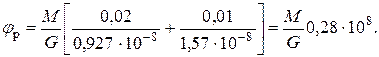
Смысл уравнения метода сил заключается в отсутствии перемещений по направлению отброшенных связей; применительно к нашей задаче речь идёт об отсутствии перемещения поворота в пра­вой заделке, т.е.

φ + φ_ρ= 0.

Отсюда определим неизвестный крутящий момент М_А = – 0,2М

(рис.1, в). Далее следует техническая работа по определению крутя­щих

моментов во всех сечениях, как 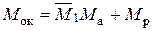(рис 1,г) и обязательной проверке окончательной эпюры М_ок, свидетельствую­щей об отсутствии поворота правой заделки:

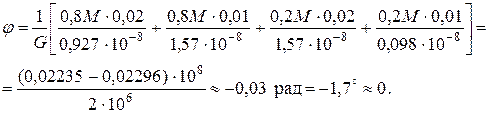
Будем считать проверку выполненной.

2. Р а с ч ё т п р о ч н о с т и в а л а. Для рассмотрения упруго- пластического деформирования вала примем график зависимости касательного напряжения от угловой деформации (диаграмму сдвига) без упрочнения (рис.3), причем τ_т = σ_т/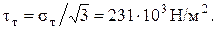

2.1. Определим моменты текучести сечений. Пластические деформации в поперечном сечении вала возникают в том случае, когда наибольшая деформация сдвига 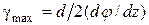достигнет γ_т, или, что то же, когда наибольшее касательное напряжение τ_mах сравняется с пределом текучести при сдвиге τ_т. При этом крутящий момент равен

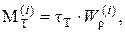
где моменты сопротивления кручению поперечных сечений равны

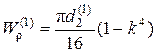, для первого участка, и 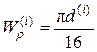- для участков

i = 2, 3, 4.