Равенство Клаузиуса. Энтропия
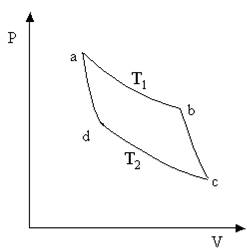 Рис. 13.1 Рис. 13.1
|
Рассмотрим какую-либо термодинамическую систему и проведем с ней цикл Карно (рис. 13.1), состоящий из изотерм a-b и c-d и адиабат b-c и d-a. Согласно теореме Карно и определению термодинамической температуры, КПД цикла Карно, независимо от природы системы, равен
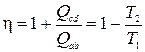 . (13.1)
. (13.1)
Здесь Т1 и Т2 температуры на изотермах, Qab = Q1 – количество тепла, полученное системой от нагревателя на изотерме a-b, Qcd = – Q2 – количество тепла, полученное системой от холодильника на изотерме c-d. Легко видеть, что соотношение (13.1) можно переписать в виде
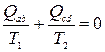 . (13.2)
. (13.2)
Отношение полученного системой количества тепла к температуре, при которой это тепло было получено, называют приведенным количеством теплоты. Как следует из соотношения (13.2) сумма приведенных количеств теплоты, полученных системой в цикле Карно, равна нулю.
 Рис. 13.2
Рис. 13.2
|
Покажем, что в любом обратимом цикле сумма приведенных количеств теплоты равна нулю. Чтобы цикл был обратимым, необходимо, чтобы на каждом его этапе температура рабочего тела бесконечно мало отличалась от температуры теплового резервуара (нагревателя или холодильника), с которым происходит теплообмен. Поэтому, вообще говоря, для проведения обратимого цикла требуется бесконечно большое число тепловых резервуаров.
Рассмотрим на P-V диаграмме произвольный обратимый цикл, изображенный на рис. 13.2. Проведем множество бесконечно близких адиабат, которые разобьют рассматриваемый цикл на «узкие» циклы, каждый из которых можно считать циклом Карно. К каждому такому циклу применим формулу (13.2). Сложив полученные выражения, придем к соотношению
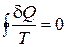 . (13.3)
. (13.3)
Это соотношение, являющееся следствием второго начала термодинамики, называется равенством Клаузиуса.
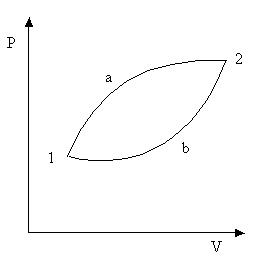 Рис. 13.3 Рис. 13.3
|
Запишем равенство Клаузиуса для обратимого цикла 1-a-2-b-1 (рис. 13.3).
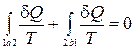 . (13.4)
. (13.4)
Учитывая обратимость цикла, соотношение (13.4) можно переписать в виде
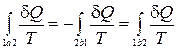 . (13.5)
. (13.5)
Независимость интеграла (13.5) от пути перехода между состояниями 1 и 2 означает, что этот интеграл представляет собой изменение некоторой функции состояния системы, названной Клаузиусом энтропией S.
Энтропия - это функция состояния термодинамической системы, изменение которой в обратимом процессе равно приведенному количеству тепла. Энтропия в термодинамике определена с точностью до произвольной постоянной. В этом отношении с определением энтропии дело обстоит так же, как с определением потенциальной энергии в механике. Физический смысл имеет не сама энтропия, а лишь разности энтропий. Разность энтропий в состояниях 1 и 2 можно найти по формуле
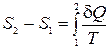 , (13.6)
, (13.6)
где интеграл вычисляется вдоль любого обратимого процесса, переводящего систему из 1 в 2.
В дифференциальной форме определение энтропии выглядит следующим образом:
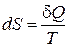 . (13.7)
. (13.7)
Используя соотношение (13.7), количество тепла, получаемое системой в бесконечно малом обратимом процессе, можно представить в виде
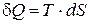 . (13.8)
. (13.8)
Подставляя это выражение в первое начало термодинамики (3.3), получим
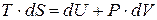 . (13.9)
. (13.9)
Это уравнение называют основным термодинамическим тождеством. Оно объединяет первое и второе начала термодинамики. Применим соотношение (13.9) для вычисления изменения энтропии n молей идеального газа при переходе из состояния (T1, V1) в состояние (T2, V2).
Для идеального газа dU = n×CV×dT, P = n×R×T/V. Подставляя dU и Р в (13.9) и деля на T, найдем
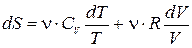 .
.
Интегрируя (при CV = const), получим
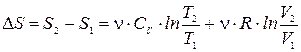 . (13.10)
. (13.10)
Дата добавления: 2017-03-12; просмотров: 4976;











