Процессы на T-S диаграмме

Формула (13.8) для элементарного количества тепла 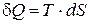весьма похожа на формулу элементарной работы .

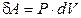Ввиду этого сходства, Гиббс предложил называть энтропию S термодинамической координатой, а температуру Т – термодинамической силой. Так же, как работа связана с изменением механической координаты (объема), подвод тепла связан с изменением термодинамической координаты – энтропии.

T   a 2   1 b   S1 S2 S Рис. 14.1

Геометрическая интерпретация количества тепла на диаграмме T-S совершенно аналогична интерпретации работы на диаграмме P-V. Полученное системой количество тепла выражается формулой

.

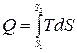Геометрически оно равно площади фигуры, лежащей под кривой, изображающей процесс (рис. 14.1). Так как температура зависит не только от энтропии, а и от других параметров состояния (объема или давления), площадь под кривой (полученное тепло) зависит не только от начального и конечного состояний, но и от всего хода процесса (Q_1a2> Q_1b2).

Рассмотрим цикл 1-а-2-b-1. На участке 1-а-2 энтропия растет, и система получает положительное количество тепла, равное площади фигуры 1-а-2-S₂-S₁-1. На участке 2-b-1 энтропия уменьшается, и система получает отрицательное количество тепла, абсолютная величина которого равна площади фигуры 2-b-1-S₁-S₂-1. Полное количество тепла Q, полученное системой при прохождении цикла, равно площади фигуры 1-а-2-b-1 (площади цикла). Так как внутренняя энергия U – функция состояния, ее изменение при обходе цикла равно нулю. Тогда из первого начала термодинамики следует, что Q = A, где А – полная работа, совершаемая системой за цикл. Таким образом, площади циклов на P-V плоскости и на T-S плоскости одинаковы.

Политропическим процессом (политропой) называют процесс, проходящей с постоянной теплоемкостью С. Найдем уравнение политропы в переменных T-S. Согласно определениям теплоемкости и энтропии, можно записать

.

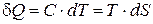Разделяя переменные, получим

.

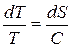Интегрируя, найдем уравнение политропы, проходящей через точку (S₀,T₀)

, .

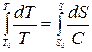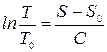Окончательно получим

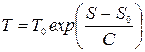. (14.1)

T C=0 C<0 CV CP   T0 C = ¥   S0 S Рис. 14.2

Таким образом, на T-S плоскости политропы с разными теплоемкостями образуют систему экспоненциальных кривых. На рис. 14.2 изображены изотерма (С = ¥), адиабата (С = 0), изохора (С = С_V), изобара (С = С_Р) и одна из политроп с отрицательной теплоемкостью (С< 0).

Подставляя в уравнение (14.1) выражение для изменения энтропии идеального газа можно получить уравнение политропы идеального газа в переменных T-V:

,

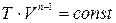где n = (C – C_P)/(C – C_V) называется показателем политропы.

В переменных P-V уравнение политропы для идеального газа имеет вид:

.

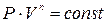Цикл Карно на T-S диаграмме всегда изображается прямоугольником, стороны которого параллельны координатным осям, тогда как на P-V диаграмме его форма зависит от вида рабочего вещества.

Докажем теорему: КПД цикла Карно больше, чем КПД любого обратимого цикла (отличного от цикла Карно), в котором максимальная температура равна температуре нагревателя, а минимальная – температуре холодильника в цикле Карно.

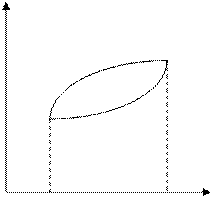
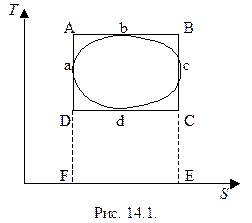Для доказательства изобразим на T-S плоскости заданный цикл abcd и опишем вокруг него цикл Карно ABCD (рис. 14.3). КПД цикла Карно

,

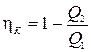где полученное от нагревателя количество тепла Q₁ изображается на диаграмме площадью прямоугольника ABFE, а тепло Q₂, отданное холодильнику, - площадью прямоугольника DCFE.

Обозначим сумму площадей фигур aAb и bBc через q₁ (q₁ > 0), а сумму площадей aDd и cCd через q₂ (q₂ > 0). Тогда КПД цикла abcd

.

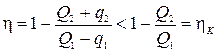Таким образом h_К > h. Теорема доказана.