Электролитическая диссоциация в растворе

Процесс распада растворенного вещества в растворе на ионы называется электролитической диссоциацией.

Первая количественная теория растворов электролитов (теория электролитической диссоциации) была высказана Аррениусом. По этой теории молекулы кислот, оснований и солей при растворении распадаются на противоположно заряженные ионы. Процесс диссоциации электролитов обратим, происходит образование молекулы из ионов, т.е. в растворе существуют ионы и молекулы. Равновесие между ионами и молекулами подчиняется закону действующих масс.

Для электролита AB, диссоциирующего в растворе на ионы по схеме

AB ⇆ A⁺ + B⁻

выражение для константы диссоциации имеет вид

K_дисс= 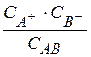(2.5)

В состоянии равновесия доля молекул, распавшихся на ионы, характеризует степень диссоциации электролита 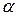, которая зависит от:

1. природы растворителя;

2. концентрации электролита;

3. температуры;

4. присутствия других растворителей.

С учетом степени диссоциации равновесные концентрации частиц будут равны

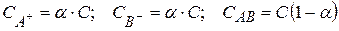
Тогда

K_дисс= 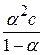(2.6)

- это уравнение называется законом разведения Оствальда и описывает поведение слабых электролитов.

При малых значениях 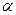можно принять, что 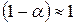, тогда

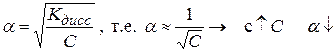(2.7)

K_дисс = f (T, природы растворителя), но не зависит от концентрации электролита в растворе.

Свойства растворов электролитов существенно отличаются от свойств идеальных растворов. Это объясняется увеличением числа частиц в растворе электролита за счет диссоциации и электролитическим взаимодействием между ними.

Вант-Гофф обнаружил увеличение осмотического давления в растворах электролитов

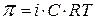(2.8)

где 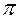– осмотическое давление

i– изотонический коэффициент Вант – Гоффа (i >1)

c– концентрация в моль/л

В водных растворах NaCI i ≈2, в BaCI₂ ~3 – он (i) показывает приближенно число ионов, на которые диссоциируют молекулы электролита.

Для слабых электролитов, при диссоциации которых образуется νионов

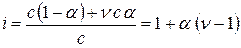(2.9)

i связан со степенью диссоциации .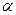

Отклонение свойств реальных растворов от свойств идеальных растворов учитывается с помощью коэффициентов активности, а концентрацию слабых электролитов заменяют на активность

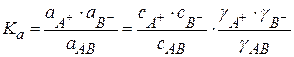(2.10)

K_a – термодинамическая константа диссоциации.

Ионы в растворах электролитов сольватированы молекулами растворителя, поэтому при написании выражений для константы диссоциации необходимо учитывать и молекулы растворителя.

Например: HA – слабый электролит, органическая кислота в водном растворе, тогда диссоциация идет по уравнению

HA + H₂O ⇆ H₃O⁺ +A^–

H₃O⁺ – ион гидроксония

K_a = 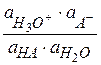(2.11)

Процесс ионизации (или диссоциации) одноосновной кислоты правильно будет представить совокупностью двух уравнений

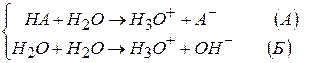
Вклад реакции (Б) в общее изменение концентрации H₃O⁺ невелик, им можно пренебречь.

Тогда

K_a = 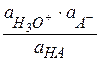или для идеальных разбавленных растворов

K_a = 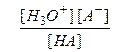, где [H₃O⁺], [A^-], [HA] - равновесные концентрации.

Значение K_a при 298 K это справочная величина.

Сложнее обстоит дело с диссоциацией двухосновных кислот (H₂S, H₂CO₃, H₂SO₃ и т.д.)

Обозначим их общей формулой H₂A

При установлении протолитического равновесия справедливы следующие реакции:

H₂A + H₂O → H₃O⁺ + HA^– (A)

HA^– + H₂O → H₃O⁺ + A^2- (Б)

H₂O + H₂O → H₃O⁺ + OH^– (B)

Вклад реакции (В) в общее изменение концентрации невелик.

При ионизации кислот по первой ступени

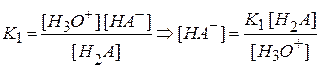
а по второй ступени

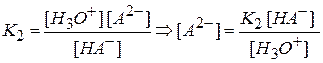
Таким образом, в растворе в равновесном состоянии одновременно могут находиться недиссоциированная кислота H₂A и ионы: HA^– и A^2-.

Уравнение материального баланса по аниону имеет следующий вид:

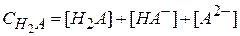
Ионные равновесия в водных растворах слабых кислот и оснований могут быть описаны с помощью распределительных диаграмм, которые показывают изменение долей различных ионных форм кислоты в зависимости от рH раствора.

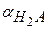– доля аналитической концентрации, приходящаяся на недиссоциированную кислоту

α_НА⁻ - доля аналитической концентрации, приходящаяся на ион HA^-

α_А⁻ - доля аналитической концентрации, приходящаяся на ион A^2-

Очевидно, что:

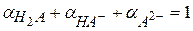
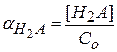, С_o – исходная концентрация кислоты;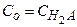

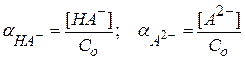
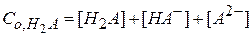
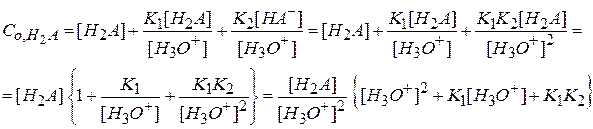
Рассчитаем доли ионных форм:

;

;

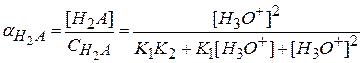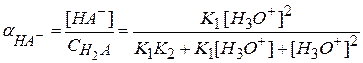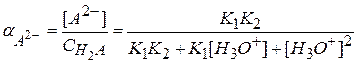
Распределение долей всех форм угольной кислоты (H₂CO₃) в зависимости от рН. (рН задается с интервалом в 1 единицу).