Механика движения подвижного состава
ТЕОРИЯ ДВИЖЕНИЯ ПОДВИЖНОГО СОСТАВА
Общие сведения.Движение подвижного состава по рельсовым путям или дорогам имеет сложный характер. Поступательное движение поезда вдоль оси пути неразрывно связано с вращением колесных пар, якорей тяговых двигателей. На это полезное поступательное перемещение подвижного состава накладываются колебательные движения экипажа, которые возникают как из-за внешних воздействий на подвижной состав со стороны пути и окружающей среды, так ив результате взаимодействия между отдельными вагонами подвижного состава и их частями, имеющими между собой упругие и жесткие связи.
Рассмотрим только полезное движение подвижного состава. Расход энергии на паразитные колебательные движения учитывается в целом путем увеличения сопротивления движению подвижного состава.
Различают три основных режима движения подвижного состава: под током (режим тяги), выбег (движение без тока) и торможение. Во всех вышеперечисленных режимах на подвижной состав действует сила тяжести и сила сопротивления движению.
В режиме тяги к подвижному составу приложена сила тяги, развиваемая тяговыми электродвигателями.
В режиме выбега тяговые двигатели отключаются от контактной сети и подвижной состав движется по инерции под действием сил сопротивления движению, направленных против движения.
В режиме торможения на подвижной состав действует направленная против движения тормозная сила.
Движение подвижного состава по рельсовому и безрельсовому пути характеризуется зависимостями скорости от пройденного пути v(l), скорости от времени v(t) и пути от времени l(t), называемых кривыми движения.
Расчет этих зависимостей производится с помощью уравнения движения подвижного состава, которое устанавливает в дифференциальной форме связь между скоростью v, временем t ипройденным путем l и дает возможность построить кривые движения.
Уравнения движения подвижного состава.При рассмотрении движения подвижного состава и выводе основного уравнения движения принимаем следующие допущения:
- подвижной состав принимают за материальную точку, которая расположена условно в центре тяжести подвижного состава;
- эта материальная точка движется поступательно под воздействием равнодействующей всех сил Fд действующих на подвижной состав. Сила Fд направлена по движению подвижного состава и может быть как положительной, так и отрицательной.
Для вывода уравнения движения подвижного состава исходим из баланса всей кинетической энергии системы. Если подвижной состав изменяет свою поступательную скорость v, то одновременно меняется и частота вращения колесных пар, зубчатых колес редуктора и якорей тяговых двигателей, т. е. изменяется их кинетическая энергия. Поэтому при составлении баланса кинетической энергии подвижного состава в целом необходимо учитывать не только кинетическую энергию, накопленную в физической массе при поступательном движении 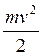 , но и кинетическую энергию, накопленную во вращающихся частях. Эта энергия, как известно из механики, для любой вращающейся массы пропорциональна ее моменту инерции J, угловой скорости ω и равна
, но и кинетическую энергию, накопленную во вращающихся частях. Эта энергия, как известно из механики, для любой вращающейся массы пропорциональна ее моменту инерции J, угловой скорости ω и равна 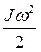 . Следовательно, кинетическая энергия подвижного состава, движущегося со скоростью v,
. Следовательно, кинетическая энергия подвижного состава, движущегося со скоростью v,
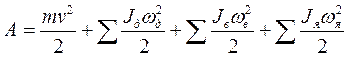 , (1)
, (1)
где Jд и ωд - соответственно момент инерции и угловая скорость движущих колесных пар и ведущих мостов подвижного состава, т. е. колесных пар и мостов, соединенных с якорями тяговых двигателей передаточными механизмами; Jв и ωв - соответственно момент инерции и угловая скорость колесных пар прицепных вагонов и ведомых мостов ПС; Jя и ωя - соответственно момент инерции и угловая скорость вращения якорей тяговых двигателей, включая части передачи, жестко связанные с валом двигателя.
Знаки суммы указывают на то, что суммирование энергии распространяется на все колесные пары и якоря тяговых двигателей подвижного состава, которые могут быть разных типов.
Выражая угловые скорости вращающихся частей через скорость поступательного движения подвижного состава радиусы колес, запишем:
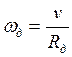 ;
; 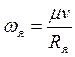 ;
; 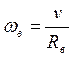 ,
,
где Rд - радиус движущих колес; Rв - радиус колес прицепного вагона и ведомых мостов ПС; μ - передаточное число редуктора.
Подставив значения угловых скоростей в выражение
(1) и вынеся за скобку 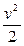 получим:
получим:
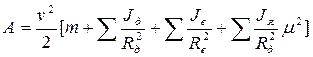 ,
,
или:
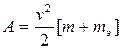 , (2)
, (2)
здесь
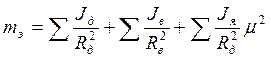
имеет размерность массы и называется эквивалентной массойвращающихся частей. Обозначив отношение эквивалентной массы к физической массе 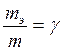 и подставив у в выражение (2), получим:
и подставив у в выражение (2), получим:
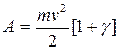 (3)
(3)
Величину ( 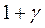 ) называют коэффициентом инерции вращающихся частей, а произведение физической массы m на этот коэффициент - приведенной массой подвижного состава mпр. Таким образом, подвижной состав с массой m эквивалентен телу, не имеющему вращающихся частей, но с массой, равной приведенной mnp = m(
) называют коэффициентом инерции вращающихся частей, а произведение физической массы m на этот коэффициент - приведенной массой подвижного состава mпр. Таким образом, подвижной состав с массой m эквивалентен телу, не имеющему вращающихся частей, но с массой, равной приведенной mnp = m( 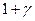 ), и движущемуся со скоростью v поступательного движения подвижного состава.
), и движущемуся со скоростью v поступательного движения подвижного состава.
Изменение кинетической энергии подвижного состава на любом участке пути равно работе действующих сил на этом участке пути, т. е. произведению силы на пройденный путь. Следовательно, если равнодействующую всех сил сопротивления движению, тяги и торможения (так называемую действующую силу) обозначить через Fд, то для бесконечно малого перемещения dl подвижногo состава получим приращение кинетической энергии
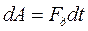
Используя выражение (3), получим:
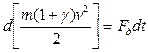 (4)
(4)
Продифференцировав выражение (4) и разделив обе части равенства на dl, получим в дифференциальной форме зависимость между скоростью движения v и пройденным путем l:
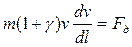 или
или 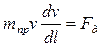 (5)
(5)
Уравнение (5) называют второй формой уравнения движения.
Для получения зависимости между скоростью v и временем t нужно подставить в уравнение (5) значение 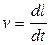 , сократить на величину dl, тогда
, сократить на величину dl, тогда
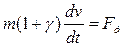 или
или 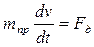 (6)
(6)
В результате получается выражение, аналогичное второму закону Ньютона, в которое вместо физической массы входит приведенная масса m( 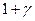 ). Уравнение (6) называют первой формой уравнения движения.
). Уравнение (6) называют первой формой уравнения движения.
Размерности величин, входящих в уравнение движения. Так как произвольно можно выбрать единицы измерения только для трех, входящих в уравнения величин, то в правые части уравнений (5) и (6) необходимо ввести переводные коэффициенты 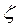 и
и 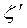 :
:
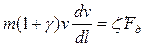 (7)
(7)
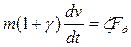 (8)
(8)
Тяговые расчеты удобнее выполнять, используя удельные значения действующей силы и ее составляющих.
Для этого делят правую часть уравнений (7) и (8) на вес подвижного состава и тогда эти уравнения принимают следующий вид:
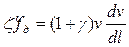 (9)
(9)
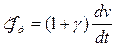 (10)
(10)
где fд - удельная действующая сила:
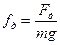
здесь т — масса подвижного состава; g — ускорение свободного падения.
Выражения (9) и (10) называются уравнениями движения в удельной форме.
Коэффициент инерции вращающихся частей.Входящий в уравнения движения коэффициент инерции вращающихся частей ( 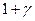 ) можно определить как экспериментальным, так и расчетным путем. На практике численное значение γ можно определить, воспользовавшись выражением:
) можно определить как экспериментальным, так и расчетным путем. На практике численное значение γ можно определить, воспользовавшись выражением:
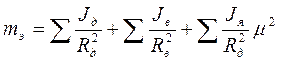 (11)
(11)
Момент инерции J каждого тела, входящий в выражение (11), представим в виде произведения:
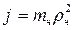 ,
,
где 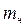 - масса вращающейся части;
- масса вращающейся части; 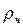 - ее радиус инерции.
- ее радиус инерции.
Тогда эквивалентная масса
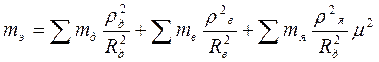 ,
,
а значение 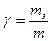
При вычислении тэ можно исходить из средних значений отношений радиусов инерции ρ к радиусам внешних окружностей вращающихся частей. Для движущих и поддерживающих колесных пар и колес 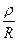 равно 0,75 - 0,80, для зубчатых колес 0,8; для якорей тяговых двигателей 0,65—0,75.
равно 0,75 - 0,80, для зубчатых колес 0,8; для якорей тяговых двигателей 0,65—0,75.
Коэффициент инерции вращающихся частей тем больше, чем меньше масса ПС и больше число вращающихся частей, а также их размеры и, следовательно, масса. Коэффициент инерции двухосных вагонов меньше, чем четырехосных. Коэффициент инерции для любого ПС с пассажирами меньше, чем без пассажиров.
ЛЕКЦИЯ 2
Дата добавления: 2017-03-12; просмотров: 3233;











