Применение уравнения движения для различных режимов движения подвижного состава

Рассмотрим уравне­ние движения применительно к различным видам движе­ния подвижного состава. Чтобы привести подвижной состав в движение, к нему нужно приложить силу тяги. Сила тяги подвижного состава F создается установлен­ными на нем тяговыми двигателями. Однако наличие только силы тяги недостаточно для управления подвиж­ным составом, так как она всегда действует в направ­лении его движения или равна нулю. Для остановки подвижного состава к нему необходимо приложить силу, направленную в сторону, противоположную дви­жению. Она создается тормозными средствами и назы­вается тормозной силой В. Сила тяги F и тормозная сила В являются управляемыми (их может регулиро­вать водитель через аппараты управления). Существуют еще неуправляемые силы. К ним относятся сила тя­жести подвижного состава G = mg и все остальные внешние силы (не поддающиеся регулированию), дей­ствующие на подвижной состав в направлении его движения или в обратном направлении. Они состав­ляют силы сопротивления движению W.

Положительным направлением для силы тяги F является направление движения подвижного состава, а для тормозной силы В и силы сопротивления движению W - направление, противоположное движению. Равно­действующей всех сил, одновременно приложенных к подвижному составу, является действующая сила

F_д = F – W - B

или в удельных величинах

,

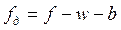где 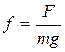- удельная сила тяги, Н/кН;

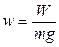- удельное сопротивление движению, Н/кН;

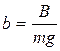- удельная тормозная сила, Н/кН;

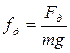- удельная действующая сила, Н/кН.

Различают три основных режима движения подвижно­го состава: тяга, выбег и торможение.

В режиме тяги к подвижному составу приложены сила тяги F и силы сопротивления движению W:

F_д = F – W.

В режиме выбега на подвижной состав действуют только силы сопротивления движению W:

F_д = – W.

В режиме торможения к подвижному составу при­ложены тормозная сила В и силы сопротивления движению W, тогда действующая сила:

F_д = -(В + W).

Все силы, действующие на подвижной состав, приложены к центру тяжести ПС.

Интегрируя уравнение движения, можно получить за­висимости скорости от пути v(l), скорости от времени v(t) и времени от пути t(l), которые называются кривыми движенияподвижного состава.

На рис. 1 приведе­ны кривые движения v(t) и v(l) для перегона с неизмен­ным профилем пути.

Рассмотрим зависимости v(t), рас­положенную слева от оси ординат, и v(l), расположен­ную справа от оси ординат, при движении по харак­терным участкам.

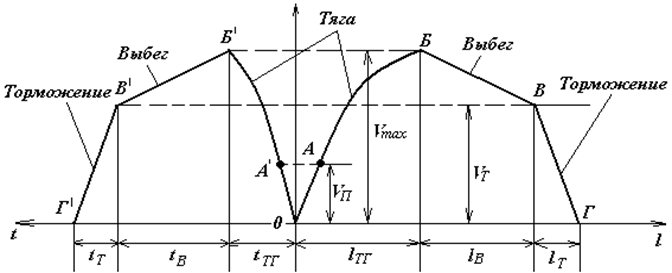
Рис. 1. Кривые движения

Режим тяги. Период тяги разделяется на периоды пуска подвижного состава ОА и ОА' и движения по авто­матической характеристике АБ и А'Б'. При пуске тяговые двигатели развивают наибольшую силу тяги, которую при неавтоматическом пуске регулирует водитель. Ее следует поддерживать в среднем постоянной. Тангенс угла наклона кривой движения v (t) к оси времени определяет ускорение подвижного состава в данный мо­мент. Если угол наклона отрезка ОА' к оси времени неиз­менен, то ускорение подвижного состава в момент пуска будет постоянным, а движение равномерно ускоренным. В момент пуска сила тяги всегда больше сопротивления движению (F > W), а действующая сила F_д = F - W положительна. Точки А и А' на кривой движения соответствуют моменту окончанию пуска и выхода на автома­тическую характеристику со скоростью v_n.

В период движения по автоматической характеристи­ке (участки АБ и А'Б') характер изменения скорости подвижного состава зависит от значения и направления действующей силы. Если действующая сила положи­тельна F_д > 0 (F > W), скорость движения будет воз­растать, но медленнее, чем при пуске, так как сила тяги с увеличением скорости уменьшается, а сопротив­ление движению возрастает. Поэтому на участке АБ (А'Б') скорость возрастает медленнее, чем на участке О А (ОА'). Точки Б и Б' соответствуют моменту выклю­чения двигателей (тока) и началу выбега.

Режим выбега. В период выбега подвижной состав движется по инерции, так как тяговые двигатели отключены, следовательно, ток и сила тяги отсутствуют (I = 0 иF = 0). Кинетическая энергия подвижного состава, накопленная в период движения под током, расходуется на преодоление сил сопротивления движе­нию. Скорость подвижного состава при движении на горизонтальном участке, подъеме и малых спусках посте­пенно уменьшается (участки БВ и Б'В'), ускорение при этом становится отрицательным. Действующая сила в период выбега будет определяться силой сопротивления движению F_д = - W. Точки В и В' соответствуют моменту окончания выбега и началу режима торможения.

Режим торможения. В период торможения соз­дается значительная тормозная сила В, направленная против движения подвижного состава. В результате скорость подвижного состава быстро уменьшается, отрицательное ускорение (тормозное замедление а_Т) по абсолютному значению велико. На кривых движения режим торможения определяется отрезками ВГ и ВГ', движение при этом равномерно замедленное, v_T — ско­рость начала торможения. Тормозное замедление харак­теризуется тангенсом наклона отрезка ВГ' к оси времени. Действующая сила при этом будет замедляющей и будет определяться суммой тормозной силы и силы сопротивления движению.

ЛЕКЦИЯ 3