Функции Бесселя первого рода
Функциями Бесселя первого рода, обозначаемыми 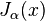 , являются решения, конечные в точке
, являются решения, конечные в точке 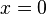 при целых или неотрицательных
при целых или неотрицательных 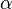 . Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых
. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых 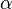 ):
):
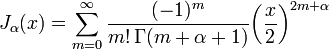
Здесь 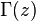 — это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально
— это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально 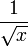 , хотя на самом деле нули функции расположены не периодично.
, хотя на самом деле нули функции расположены не периодично.
Ниже приведены графики 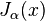 для
для 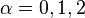 :
:
Если 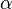 не является целым числом, функции
не является целым числом, функции 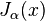 и
и 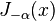 линейно независимы и, следовательно, являются решениями уравнения. Но если
линейно независимы и, следовательно, являются решениями уравнения. Но если 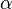 целое, то верно следующее соотношение:
целое, то верно следующее соотношение:
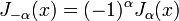
Оно означает, что в этом случае функции линейно зависимы. Тогда вторым решением уравнения станет функция Бесселя второго рода.
Можно дать другое определение функции Бесселя для целых значений 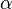 , используя интегральное представление:
, используя интегральное представление:
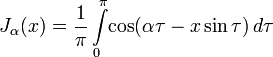
Этот подход использовал Бессель, изучив с его помощью некоторые свойства функций. Возможно и другое интегральное представление:
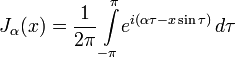
Дата добавления: 2017-03-12; просмотров: 1317;










