Предмет и задачи математической физики.

Методы математической физики начали формироваться при изучении колебаний струн и стержней, а также решении задач, связанных с акустикой и термодинамикой. Позднее идеи математической физики получили новое развитие в связи с задачами теплопроводности, диффузии, упругости, оптики и электродинамики. В ХХ-м веке в математическую физику включаются задачи квантовой физики и теории относительности, а также новые проблемы газовой динамики, переноса частиц и физики плазмы.

Многие задачи классической математической физики сводятся к краевым задачам для дифференциальных (интегрально-дифференциальных) уравнений.

Основными математическими средствами исследования этих задач служат теория дифференциальных уравнений, теория функций, функциональный анализ, теория вероятностей, вычислительная математика.

Среди задач математической физики выделяется важный класс корректно поставленных задач, то есть задач, для которых решение существует, единственно, и непрерывно зависит от данных задачи.

Доказательство корректности – это первая апробация математической модели:

1. модель непротиворечива (решение существует);

2. модель однозначно описывает физический процесс (решение единственно);

3. модель мало чувствительна к погрешностям измерений физических величин (решение непрерывно зависит от данных задачи).

1.2 Дифференциальные операторы математической физики.

Градиент – векторная функция, аргументом которой является скалярная функция точки:

;

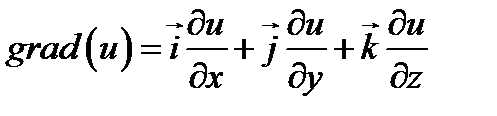производная по направлению : ;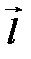

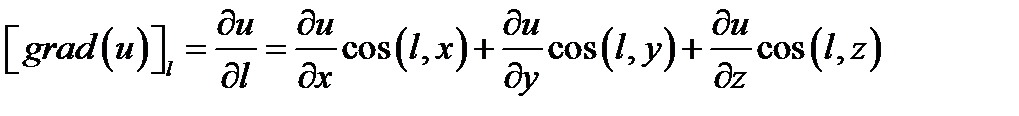очевидно, что .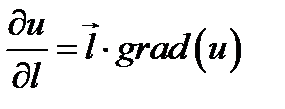

Дивергенция – скалярная функция аргументом, которой является векторная функция точки :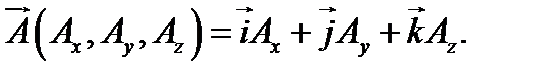

.

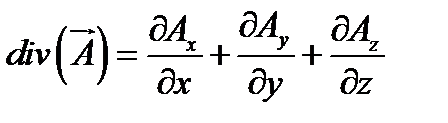Ротор (вихрь) – векторная функция, аргументом которой является векторная функция точки.

,

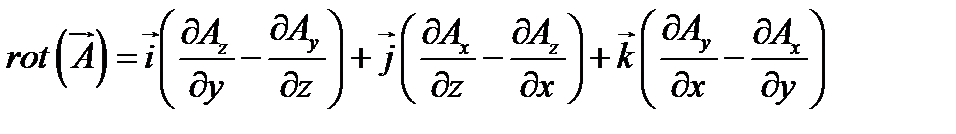удобно выразить в виде .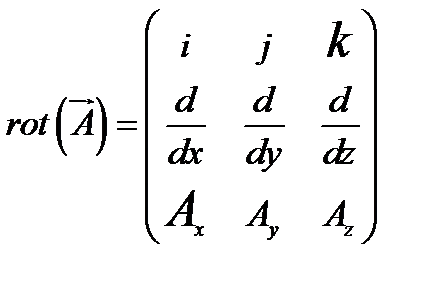

Оператор Гамильтона (оператор набла) - ;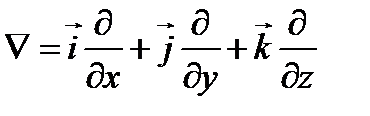

применительно к скаляру ;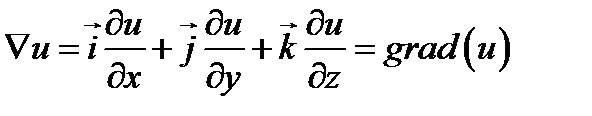

применительно к векторной функции ;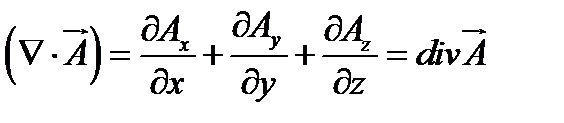

векторное произведение 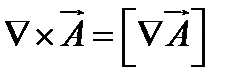двух векторов дает:

;

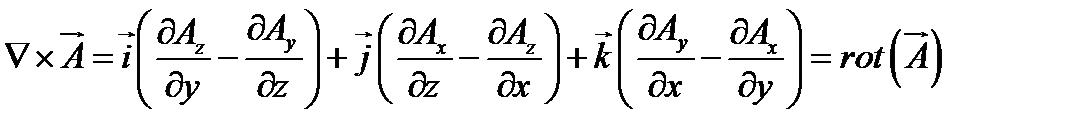Оператор Лапласа (лапласиан) – оператор вида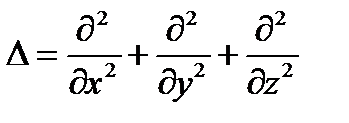

применительно к скалярной функции ;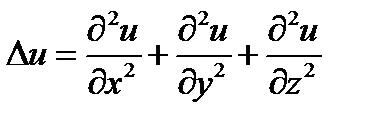

применительно к векторной функции ,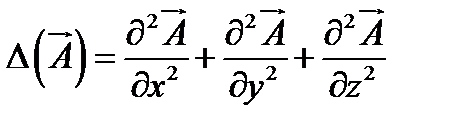

так как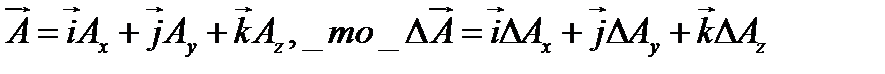

аналогично получаем .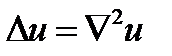

Дифференциальные операторы в криволинейных системах координат.

1. Полярная система координат.

Координаты полярной с.к.:

угловая величина - 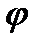; радиус-вектор - .

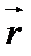Оператор Лапласа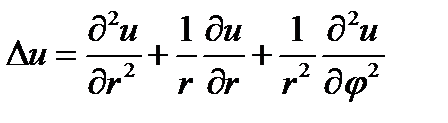

2. Цилиндрическая система координат

Координаты цилиндрической с.к.:

радиус-вектор - 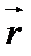; угловое отклонение - 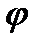; высота -z .

Оператор Лапласа .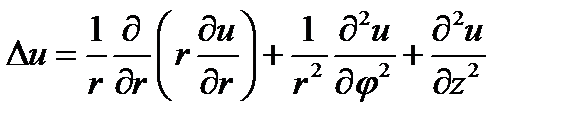

3. Сферическая система координат

Координаты сферической с.к.:

радиус-вектор - 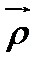; угловое отклонение - 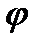; отклонение по высоте - .

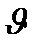Оператор Лапласа: .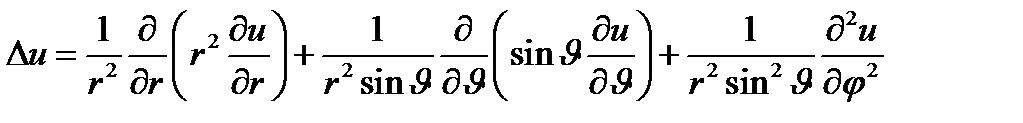

Раздел 2.Уравнения и задачи математической физики.

2.1. Уравнения колебаний:

а) поперечные колебания струны:

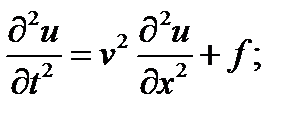
где: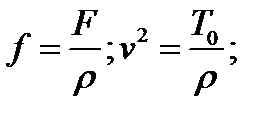

б) продольные колебания упругого стержня:

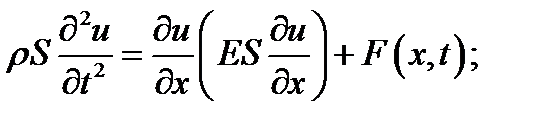
где: 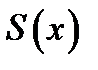- площадь поперечного сечения стержня;

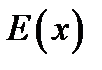- модуль Юнга в точке ;

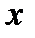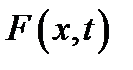- внешнее усилие.

в) поперечные колебания мембраны:

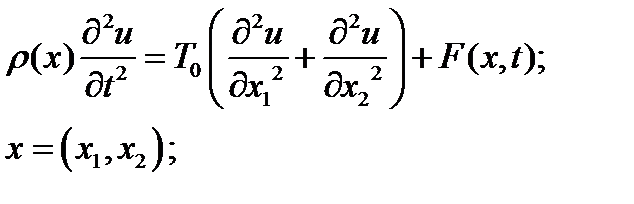
если 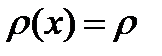, тогда уравнение колебаний мембраны выглядит так:

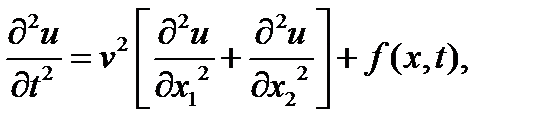
где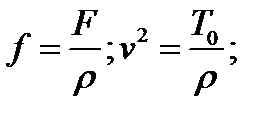

граничные условия:

для жестко закрепленных краев -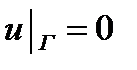

начальные условия:

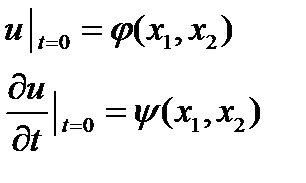
г) трехмерное волновое уравнение:

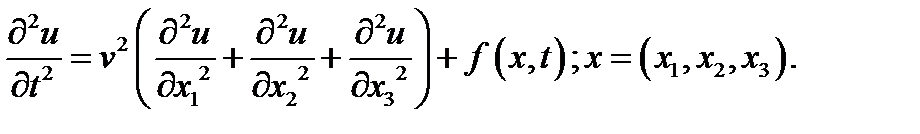
д) телеграфное уравнение:

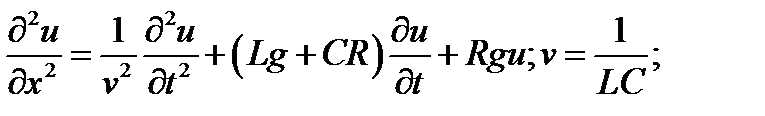
где 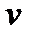- скорость передачи сигнала по кабелю.

2.2. Уравнение диффузии и теплопроводности:

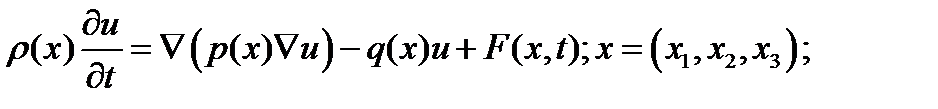
Закон Фурье -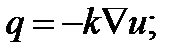

2.3. Стационарные уравнения:

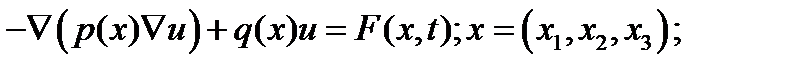
при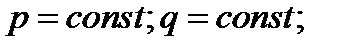

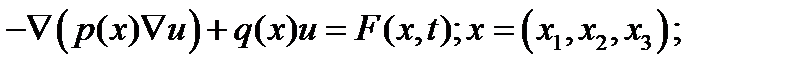
переходит в уравнение Пуассона: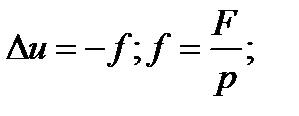

при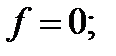

переходит в уравнение Лапласа: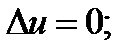

а) уравнение электростатики:

заряд в единице объема -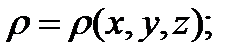

вектор напряженности электрического поля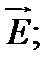

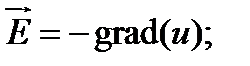
где 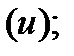- потенциал электростатического поля.

б) уравнение гидродинамики.

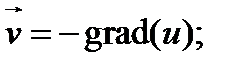
где 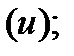- потенциал скорости;

2.4. Классификация уравнений второго порядка:

а) классификация уравнений в точке;

б) классификация уравнений с двумя независимыми переменными.

2.5. Преобразование уравнений второго порядка с помощью замены переменных:

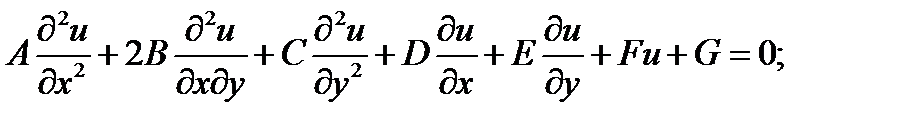
где 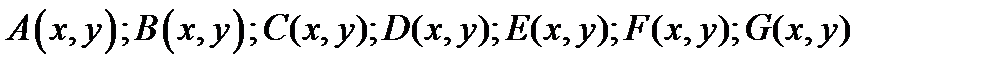- заданные функции от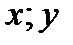

а) в уравнения гиперболического типа;

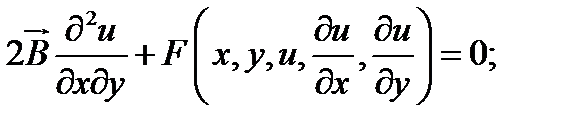
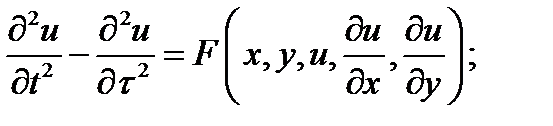
б) в уравнения параболического типа;

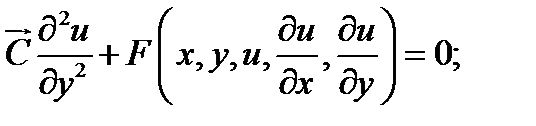
в) уравнения эллиптического типа.

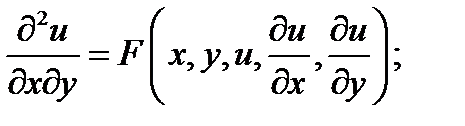
преобразуется к виду:

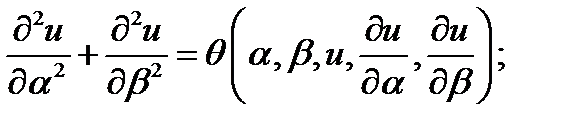
1. Составить квадратичную форму уравнения:

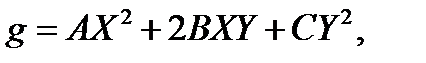
2. Определитель квадратичной формы:

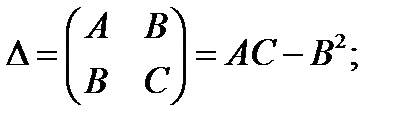
а) 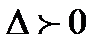, , 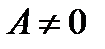тогда можно записать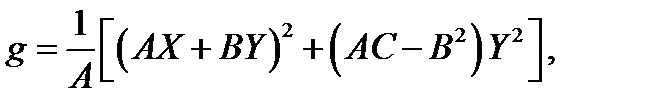

форма определенная и уравнение принадлежит к эллиптическому типу;

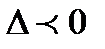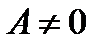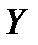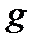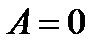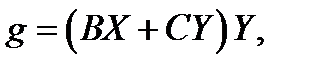б) возможны 2 случая, когда и в зависимости от знак меняется, то уравнение принадлежит к гиперболическому типу, если , то форма 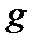- неопределенная и уравнение принадлежит к гиперболическому типу.

в) 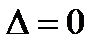тип уравнения – параболический.

3. Составляем характеристическое уравнение: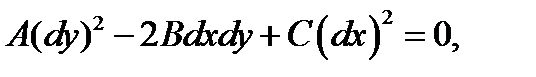

и определяем корни этого характеристического уравнения

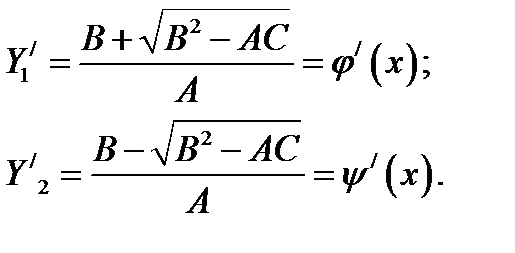
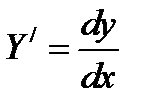
4. Определяем новые переменные:

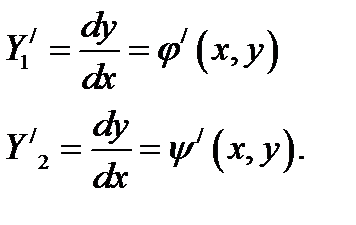
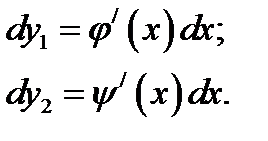
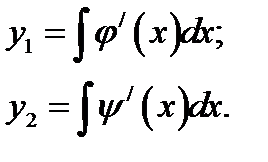
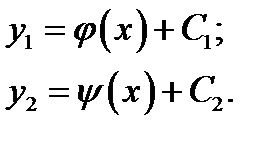
а) для уравнения гиперболического типа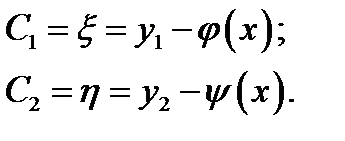

б) для уравнения эллиптического типа вводим переменные α и β

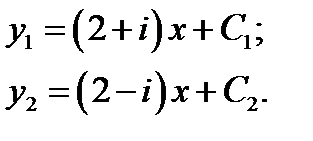
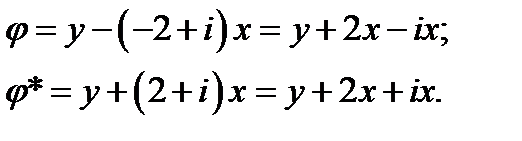
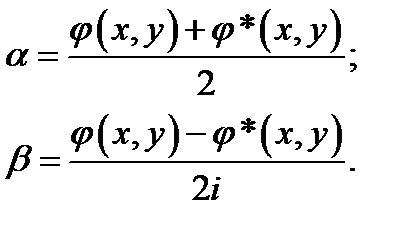
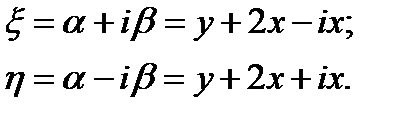
в) для уравнения параболического типа т.к. корень единственный 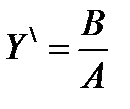выбираем переменные: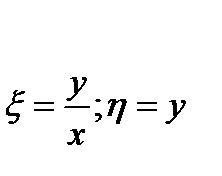

5. Находим частные производные по переменным 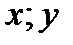для чего дифференцируем

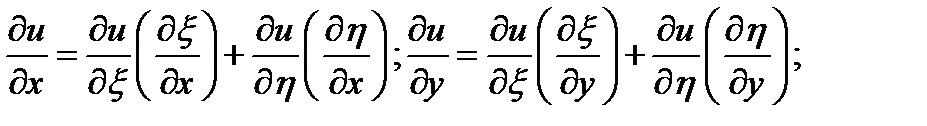
производные в (…) нужно посчитать, без (…) записать в общем виде.

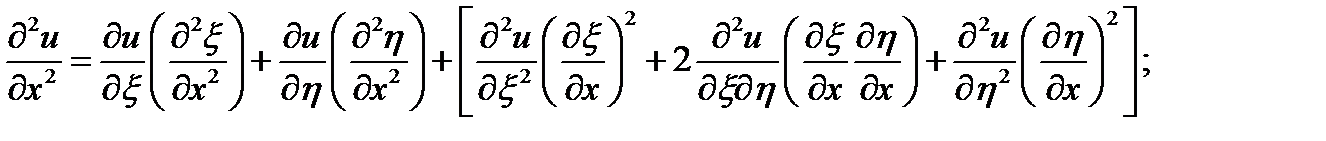
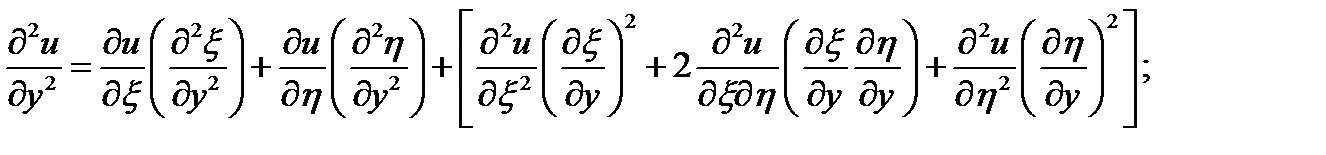
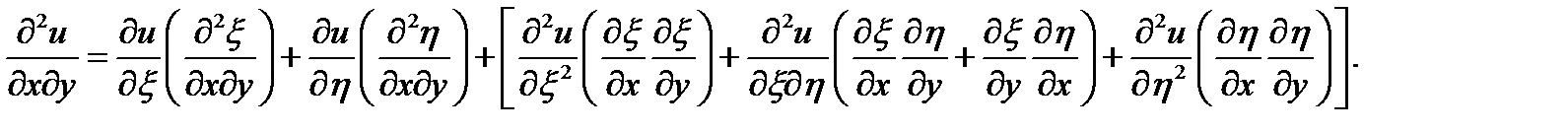
Постоянные в уравнениях канонической формы:

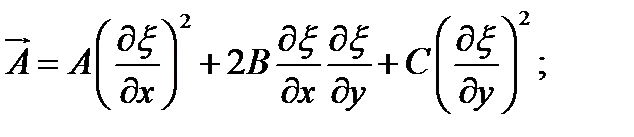
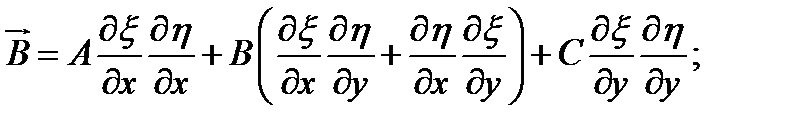
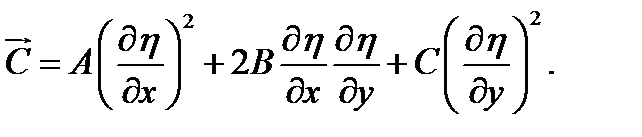
2.6. Классификация задач математической физики:

а) задача Коши для уравнений гиперболического типа -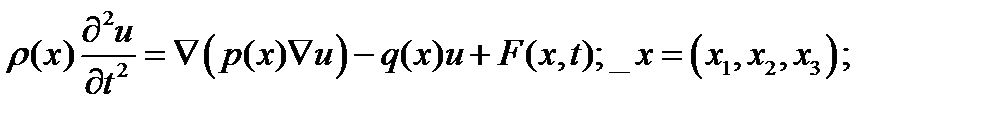

ставится следующим образом:

найти функцию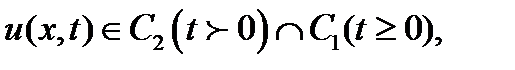

удовлетворяющую уравнению данного типа, в полупространстве при 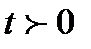, и начальным условиям при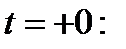

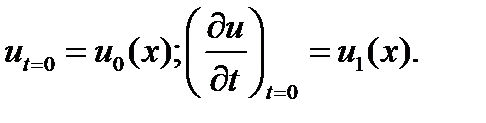
Для уравнений диффузии и теплопроводности параболического типа -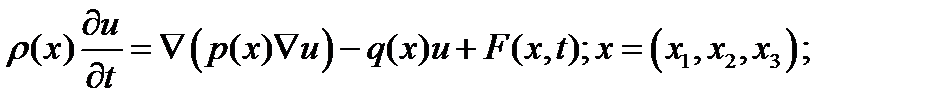

задача Коши ставится следующим образом:

найти функцию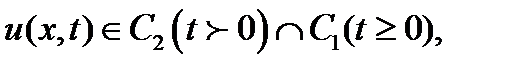

удовлетворяющую уравнению этого типа, в полупространстве при 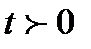, и начальным условиям при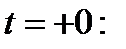

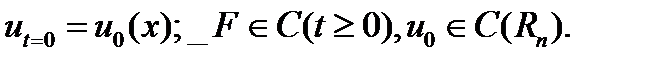
б) краевая задача для уравнений эллиптического типа –

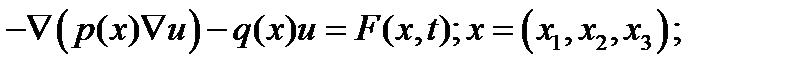
ставится следующим образом:

найти функцию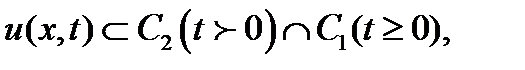

удовлетворяющую уравнению данного типа, в области 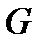и граничным условиям на границе 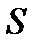следующего вида:

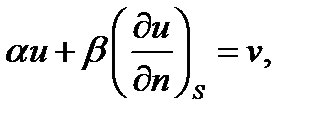
где 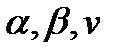заданные непрерывные функции на 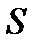причем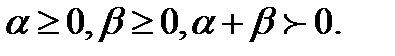

Граничное условие 1-го рода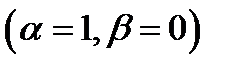

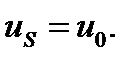
Граничное условие 2-го рода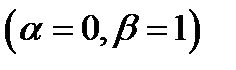

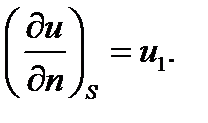
Граничное условие 3-го рода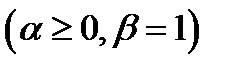

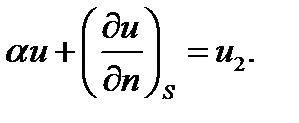
Для уравнения Лапласа и уравнения Пуассона краевая задача первого рода называется задачей Дирихле: найти функцию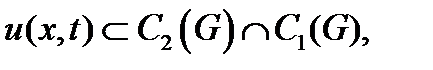

удовлетворяющую, в области 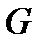уравнению 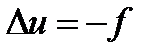и граничному условию на поверхности .

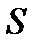Граничное условие 1-го рода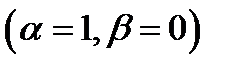

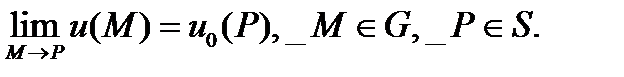
Граничное условие 2-го рода:

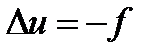
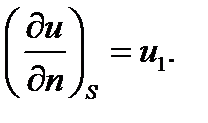
называется задачей Неймана: найти функцию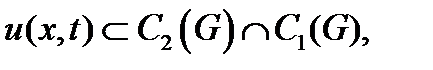

удовлетворяющую, в области 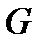уравнению 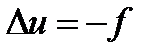или 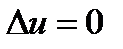и граничному условию на поверхности .

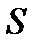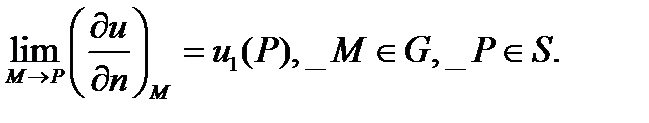
Функция 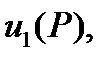должна удовлетворять дополнительному условию разрешимости задачи Неймана. Воспользуемся равенством

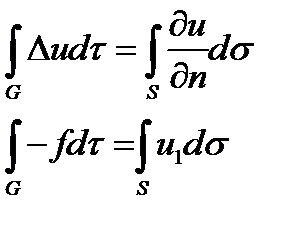
В уравнении Лапласа условие разрешимости принимает вид:

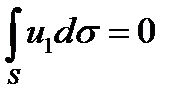
Используется теорему о среднем 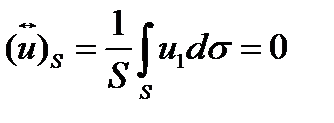, - среднее значение функции .

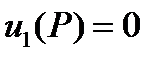Краевые задачи 1-го, 2-го, 3-го рода для уравнения Лапласа носят названия гармонических краевых задач.

в) смешанная задача для уравнения колебаний гиперболического типа –

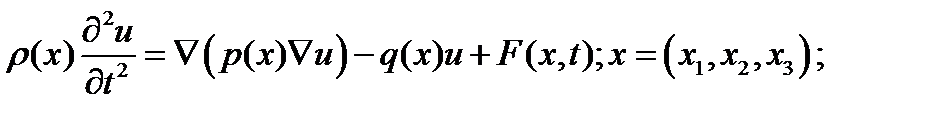
ставится следующим образом:

найти функцию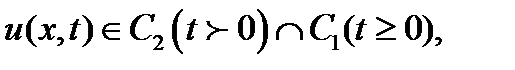

удовлетворяющую уравнению данного типа, в полупространстве при 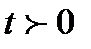, и начальным условиям пр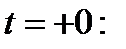и и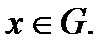

при этом должны выполняться условия гладкости:

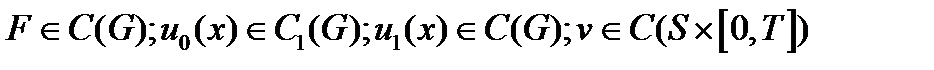
и условия согласованности:

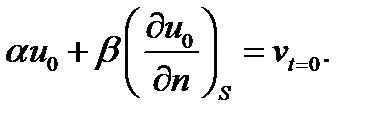
2.7. О корректности поставленной задачи и единственности решения задачи математической физики.

1. Решение должно существовать в каком-то классе функций М₁ .

2. Решение должно быть единственным в некотором классе функций М₂

3. Решение должно нейтрально зависеть от данных задачи (начальных и граничных условий, свободного члена, коэффициентов уравнения).

2.8. Теорема существования и единственности решения задачи Коши. Основные классы уравнений, интегрируемых в квадратурах.

2.9. Понятие об общем интеграле уравнения в частных производных.

Рассмотрим практически определение общих интегралов некоторых дифференциальных уравнения в частных производных:

Пример 1.Задана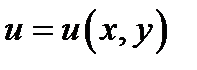

и диф. уравнение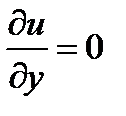

следовательно любая произвольная функция - 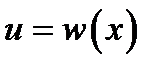является решением данного уравнения.

Пример 2. Задано диф. уравнение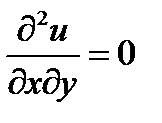

можно получить решение общего вида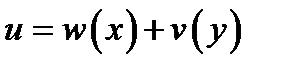

где 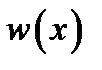, 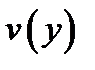произвольные дифференцируемые функции.

Пример 3. Задана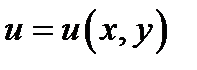

и диф. уравнение ;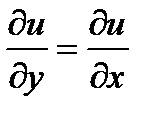

проведем замену переменных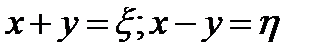

найдем частные производные:

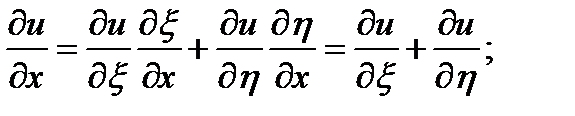
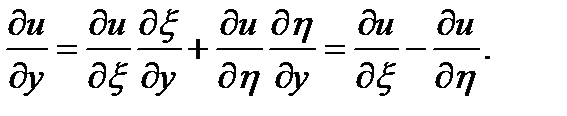
получаем уравнение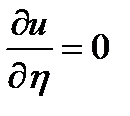

следовательно 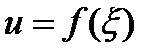получаем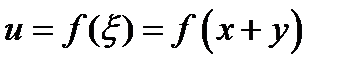

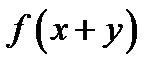- любая дифференцируемая функция.

Пример 4. Задано диф. уравнение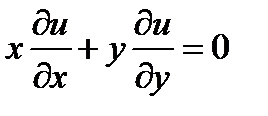

проведем замену переменных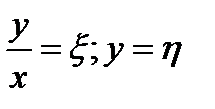

найдем частные производные:

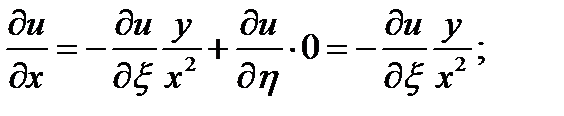
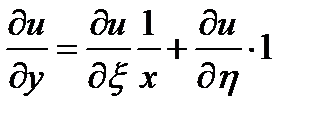
уравнение принимает вид 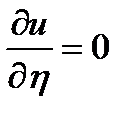решением является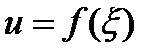

любая дифференцируемая функция .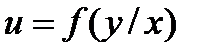

Пример 5 . Задано диф. уравнение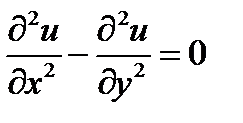

проведем замену переменных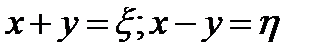

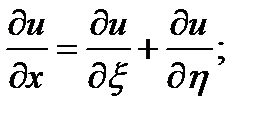
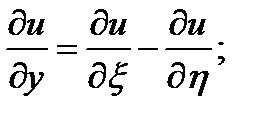
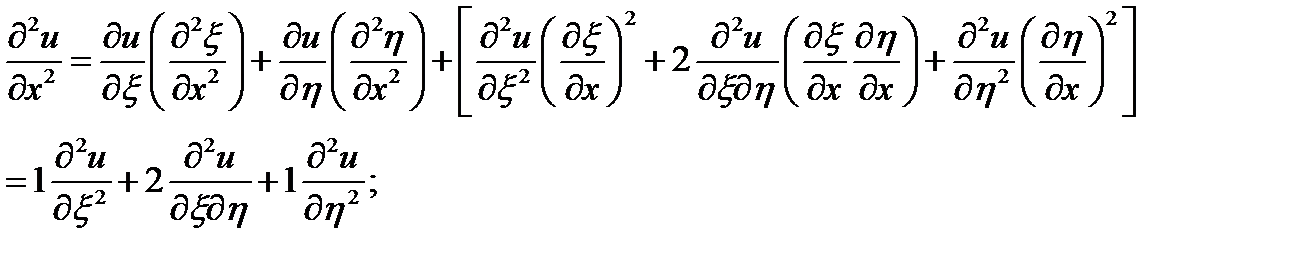
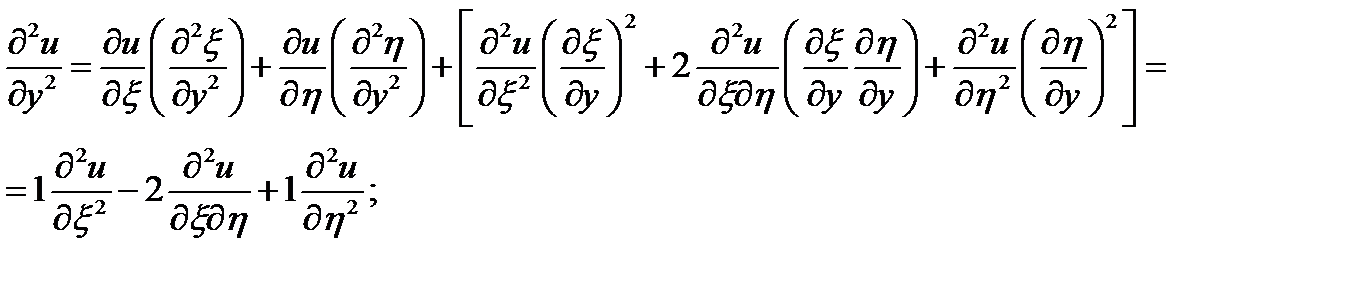
уравнение принимает вид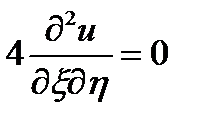

следовательно, общий интеграл уравнения будет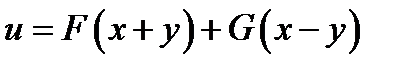

где F и G – любые дифференцируемые функции.

Пример 6 . задано уравнение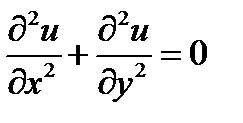

решение найдем в виде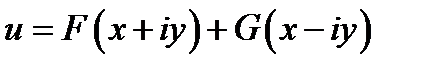

где F и G – любые дифференцируемые функции