КОНВЕКТИВНОГО ТЕПЛООБМЕНА

Дифференциальное уравнение теплоотдачи выводится на основании анализа условий теплообмена в месте соприкосновения теплоносителя с поверхностью обтекаемого тела. Как отмечалось выше, при конвективном теплообмене у поверхности тела всегда имеется тонкий ламинарный подслой теплоносителя, скорость движения в котором близка к нулю, и поэтому перенос теплоты в нём осуществляется только за счёт теплопроводности. Применим для этого подслоя закон Фурье.

Примем, что ось «у» направлена по нормали к поверхности тела. Тогда по закону Фурье ,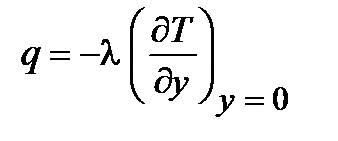

где условие у = 0 означает, что производная определяется у поверхности тела. С другой стороны, конвективный теплообмен описывается формулой Ньютона 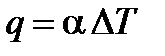. Приравнивая правые части этих формул, получим

.

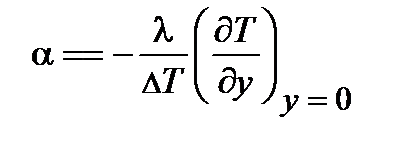Это уравнение и является дифференциальным уравнением теплоотдачи.

Уравнение переноса теплоты. Перенос теплоты в неподвижной среде (твердом теле) описывается дифференциальным уравнением теплопроводности .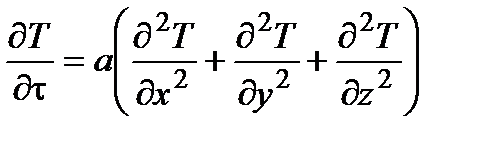

В нем левая часть 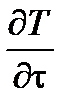представляет собой изменение температуры в фиксированном элементе тела во времени.

В движущейся среде изменение температуры частицы теплоносителя является следствием двух обстоятельств - изменения температуры во времени и изменения ее вследствие перемещения частицы из одной точки пространства в другую.

Переход от неподвижной среды к движущейся должен быть произведен путем замены частной (локальной) производной 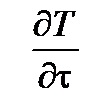на полную 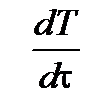. Тогда уравнение переноса теплоты в движущейся среде при ламинарном течении теплоносителя примет вид: ,

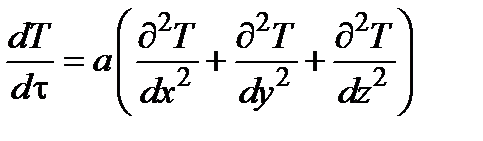где а – коэффициент температуропроводности.

Раскроем величину полной производной:

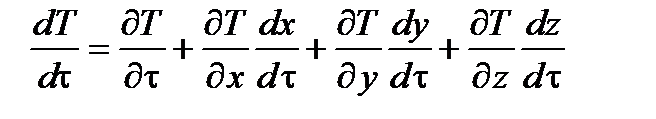, или ,

где c_х = dx/dt, c_y = dy/dt, c_z = dz/dt - проекции скорости движения теплоносителя (относительно омываемой поверхности) на оси х, у, z.

Первый член в правой части последнего уравнения представляет собой скорость изменения температуры в той точке пространства, в которой находится рассматриваемый элементарный объем теплоносителя в данный момент времени, а сумма остальных членов - изменение температуры, обусловленное перемещением этого объема из одной точки пространства в другую, т. е. вследствие конвекции.

Используя значение 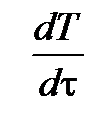, получим дифференциальное уравнение переноса теплоты в движущейся среде

.

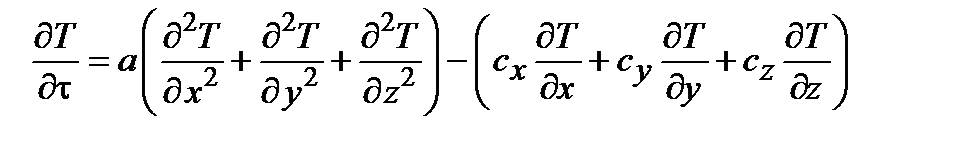В правой части этого уравнения первый член определяет скорость изменения температуры в данной точке пространства вследствие переноса теплоты теплопроводностью, а второй - вследствие переноса теплоты конвекцией.

Уравнение движения теплоносителя. Как следует из последнего уравнения, протекание процесса конвективного теплообмена зависит от распределения скоростей теплоносителя около обтекаемого им тела. Определить это поле скоростей позволяет дифференциальное уравнение движения теплоносителя – уравнения Навье-Стокса в следующем виде:

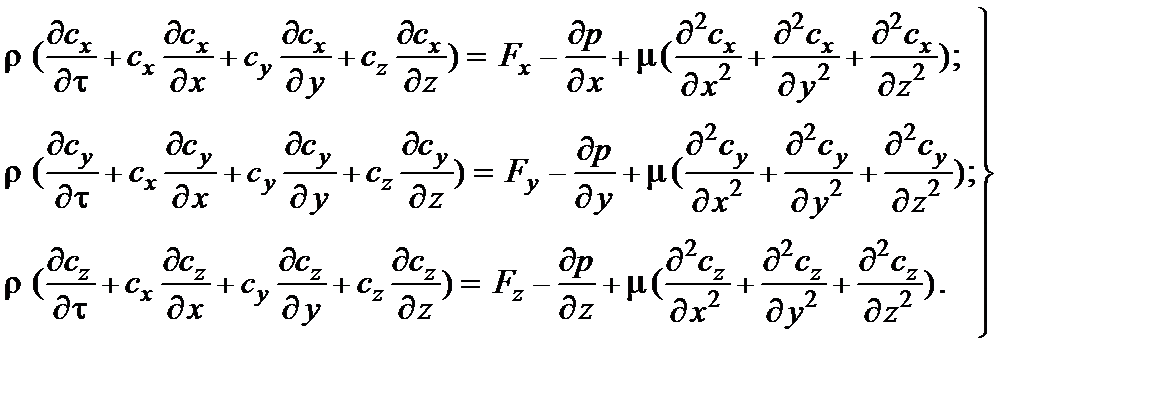
Здесь F_х , F_у , F_z - проекции массовой силы 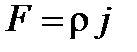, действующей на единицу объёма (j - ускорение, соответствующее этой массовой силе).

Система рассмотренных выше дифференциальных уравнений теплоотдачи, переноса теплоты и движения теплоносителя, дополненная уравнением неразрывности, описывает бесконечное множество процессов конвективного теплообмена. Для математического описания конкретного процесса теплоотдачи к этой системе уравнений необходимо присоединить краевые условия данного процесса. Это требует, во-первых, определить параметры потока в начальный момент времени (начальные условия, t = 0) и, во-вторых, установить граничные условия, т.е. параметры невозмущенного набегающего потока теплоносителя и условия на омываемых им поверхностях. В этом случае решение описанной системы уравнений позволит определить значения скоростей, температур, коэффициентов теплоотдачи и плотности теплового потока во всей рассматриваемой области.