Первая теорема подобия. Критерии подобия
Первая теорема подобия: у подобных физических явлений одноименные критерии подобия численно одинаковы.
Критериями подобия называются безразмерные комплексы, составленные из размерных величин, характеризующих данное явление.
Вывод критериев подобия производится из уравнений, описывающих это явление.
Докажем первую теорему подобия на примере процесса теплоотдачи. Пусть в каждой из двух систем теплоотдача описывается уравнением теплоотдачи в виде 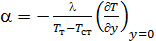 .
.
Приведем это уравнение к безразмерному виду, введя следующие безразмерные переменные: 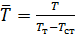 ;
; 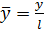 .
.
Тогда получим 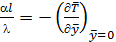 ,
,
где 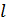 - характерный линейный размер тела, например, длина хорды профиля.
- характерный линейный размер тела, например, длина хорды профиля.
Но у подобных явлений безразмерные поля одноименных величин тождественно равны, т.е. 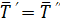 ,
, 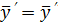 . Тогда правые части уравнений
. Тогда правые части уравнений
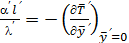 и
и 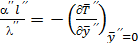 ,
,
описывающих эти явления, одинаковы. Следовательно одинаковы и левые части, т.е. 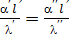 .
.
Аналогичный анализ уравнения переноса тепла приводит к равенству следующих безразмерных комплексов
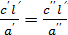 ,
,
где 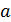 - коэффициент температуропроводности.
- коэффициент температуропроводности.
Эти безразмерные комплексы называются критериями подобия. Им присвоены следующие обозначения и названия.
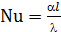 - критерий Нуссельта. Это безразмерный коэффициент теплоотдачи. Он характеризует интенсивность конвективного теплообмена.
- критерий Нуссельта. Это безразмерный коэффициент теплоотдачи. Он характеризует интенсивность конвективного теплообмена.
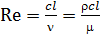 - Критерий Рейнольдса. Характеризует соотношение между силами инерции и вязкости потока, т.к.
- Критерий Рейнольдса. Характеризует соотношение между силами инерции и вязкости потока, т.к. 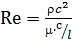 . Если
. Если 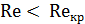 - поток ламинарный, если
- поток ламинарный, если 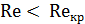 - поток турбулентный.
- поток турбулентный.
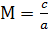 - число Маха. Характеризует сжимаемость газового потока.
- число Маха. Характеризует сжимаемость газового потока.
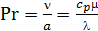 - критерий Прандтля – физический параметр вещества. Он характеризует связь между процессами переноса теплоты и механической энергии, т.е. связь между полями скоростей и температур.
- критерий Прандтля – физический параметр вещества. Он характеризует связь между процессами переноса теплоты и механической энергии, т.е. связь между полями скоростей и температур.
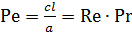 - Характеризует доли переноса теплоты за счет теплопроводности и конвекции.
- Характеризует доли переноса теплоты за счет теплопроводности и конвекции.
Таким образом, в подобных процессах конвективного теплообмена при вынужденном движении теплоносителя критерии 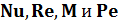 имеют численно одинаковые значения.
имеют численно одинаковые значения.
Это записывается следующим образом:
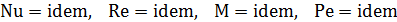 .
.
В некоторых случаях условия подобия упрощаются. Например, при малых скоростях теплоносителя (газа) влиянием числа М, характеризующего сжимаемость, можно пренебречь.
Таким образом, равенство одноименных критериев подобия является следствием подобия физических явлений.
С другой стороны, равенство критериев подобия в двух явлениях одинаковой природы при наличии геометрического подобия обеспечивает подобие этих физических явлений.
Дата добавления: 2021-06-28; просмотров: 635;











