Понятие о начальной окружности.
На каждом зубчатом колесе, сопряжено работающем в паре, обязательно есть такие окружности, которые обкатываются одна по другой без скольжения. Такими окружностями являются окружности, сопрягаемые в полюсе зацепления. Эти окружности называются начальными окружностями.
В нашем случае это окружности 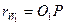 и
и 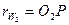 . Если колёса не корректированы, то начальные окружности совпадают с делительными. Если колёса в передаче корректированы, то
. Если колёса не корректированы, то начальные окружности совпадают с делительными. Если колёса в передаче корректированы, то 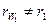 и
и 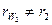 . При корректировании могут быть исправлены межцентровое расстояние
. При корректировании могут быть исправлены межцентровое расстояние 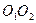 . Центры
. Центры 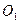 и
и 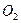 могут быть разведены или сближены, в зависимости от требований. В таких колёсах постоянными остаются диаметры делительных окружностей
могут быть разведены или сближены, в зависимости от требований. В таких колёсах постоянными остаются диаметры делительных окружностей 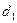 и
и 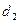 , и появляются диаметры начальных окружностей
, и появляются диаметры начальных окружностей 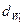 и
и 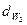 .
.
На отдельно взятом колесе отсутствует начальная окружность, она появляется только в процессе сопряжено работающих колёс.
На зубчатом колесе следует различать пять окружностей:
1. Делительная окружность 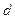 .
.
2. Начальная окружность 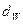 (в сопряжённой передаче).
(в сопряжённой передаче).
3. Основная окружность 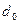 (окружность от которой строится эвольвента).
(окружность от которой строится эвольвента).
4. Окружность выступов 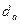 .
.
5. Окружность впадин 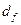 .
.
Основные понятия и определения из теории зацепления.
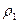
 и
и 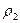 - радиусы основных окружностей.
- радиусы основных окружностей.
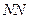 - общая касательная к основным окружностям.
- общая касательная к основным окружностям.
Изобразим сопряжённые профили у полюса зацепления. Так как линия 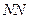 является общей касательной к основным окружностям, то, исходя из геометрии построения эвольвенты, профили зубьев всегда будут касаться только на этой линии. Линия
является общей касательной к основным окружностям, то, исходя из геометрии построения эвольвенты, профили зубьев всегда будут касаться только на этой линии. Линия 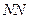 всегда будет перпендикулярна к сопряжённым профилям. Поэтому линию
всегда будет перпендикулярна к сопряжённым профилям. Поэтому линию 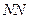 принято называть линией зацепления.
принято называть линией зацепления.
Линия зацепления – геометрическое место точек контакта двух сопряжено работающих профилей.
На линии 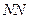 различают теоретический и рабочий участки линии зацепления.
различают теоретический и рабочий участки линии зацепления.
Теоретический участок – отрезок между основаниями перпендикуляров, опущенных на линию зацепления 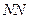 из центров.
из центров.
Практический или рабочий участок – участок линии зацепления, ограниченный внешними окружностями колёс.
Если за пределами теоретического участка частично окажется рабочий участок, то нарушится постоянство передаточного соотношения. Чтобы передаточное отношение было постоянным необходимо, чтобы рабочий участок находился в пределах теоретического.
Изобразим профили зубьев в момент встречи и расставания, и отметим на начальной окружности положение профилей при встрече и расставании. Дуга 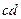 на начальной окружности есть путь
на начальной окружности есть путь 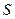 в процессе контакта. Дуга
в процессе контакта. Дуга 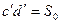 - дуга зацепления на основной окружности.
- дуга зацепления на основной окружности.
Коэффициент перекрытия 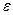 - коэффициент, показывающий количество шагов, укладывающихся в дуге зацепления,
- коэффициент, показывающий количество шагов, укладывающихся в дуге зацепления, 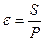 .
.
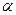 - угол зацепления. Угол зацепления гостирован, так как положение нормали определяет кривизну профиля.
- угол зацепления. Угол зацепления гостирован, так как положение нормали определяет кривизну профиля.
Коэффициент перекрытия оптимален, если он больше единицы. Чем больше коэффициент перекрытия 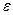 , тем лучше работает передача, то есть улучшается плавность зацепления. Если коэффициент перекрытия меньше единицы, то встречи и расставания зубьев будут сопровождаться ударами.
, тем лучше работает передача, то есть улучшается плавность зацепления. Если коэффициент перекрытия меньше единицы, то встречи и расставания зубьев будут сопровождаться ударами.
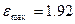 при
при 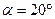 ;
; 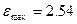 при
при 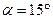 .
.
Численное значение коэффициента перекрытия 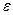 показывает количество пар зубьев, одновременно находящихся в зацеплении. Если
показывает количество пар зубьев, одновременно находящихся в зацеплении. Если 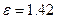 , то в процессе зацепления 42 процента времени в контакте между колёсами находится две пары зубьев, а остальные 58 процентов времени контакт между колёсами осуществляется только одной парой зубьев.
, то в процессе зацепления 42 процента времени в контакте между колёсами находится две пары зубьев, а остальные 58 процентов времени контакт между колёсами осуществляется только одной парой зубьев.
В технике более распространены передачи с углом зацепления 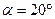 , поскольку габариты передачи в этом случае получаются меньше, чем при угле зацепления
, поскольку габариты передачи в этом случае получаются меньше, чем при угле зацепления 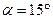 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Геометрические параметры зубчатых колёс. | | | Эпициклические зубчатые передачи. |
Дата добавления: 2017-02-13; просмотров: 3601;











