Геометрические параметры зубчатых колёс.

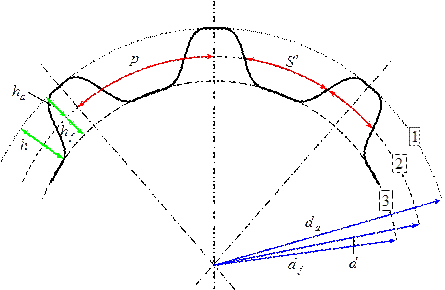
Кинематическими характеристиками всякого колеса являются число зубьев 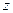и шаг зацепления .

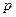1 – наружная окружность .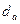

2 – делительная окружность .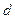

3 – окружность впадин .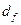

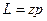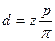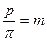Если дано число зубьев и длина шага, то длину делительной окружности можно найти по формуле: , тогда диаметр делительной окружности определяется с помощью выражения , где - модуль зацепления, то есть .

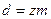Через модуль зацепления 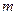выражаются все геометрические параметры зубчатого колеса и межосевые расстояния передач. Модуль зацепления является гостированной величиной, поскольку профильный инструмент для изготовления зубчатых колёс и измерительные инструменты дорогостоящи.

Делительная окружность делит зуб на две части: ; ; .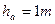

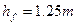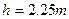Определяем диаметры колёс:

;

.

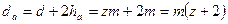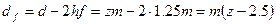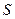- толщина зуба.

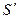- ширина впадины.

Теоретически толщина зуба должна быть равна ширине впадины, но, чтобы не было защемления при зацеплении, на практике ширина впадины делается больше, чем толщина зуба в пределах допуска на боковой зазор.

Межосевое расстояние в передачах принято обозначать : .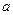

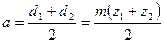Основная теорема зацепления.

Теорема Виллиса.

; .

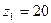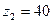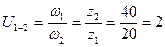
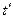- время полного контакта двух сопряжёно работающих зубьев, от встречи до расставания. Внутри этого промежутка заметно, что передаточное отношение 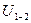будет переменным. Если зубчатая передача быстроходна, то такие передачи непригодны.

Теорема Виллиса.

Какой кривой необходимо очертить профили зубьев, чтобы мгновенное передаточное отношение было постоянным?

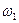Известны угловые скорости и .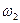

; .

; .

.

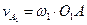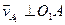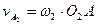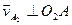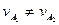Через точку 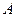проведём общую касательную 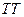к сопряжённым профилям. Разложим вектора скоростей на нормальные и тангенциальные составляющие, и сравним нормальные составляющие скоростей. Возможны следующие варианты:

1. 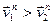- первый профиль «внедрится» во второй, что приведёт к их разрушению.

2. 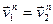- профили работают в контакте.

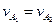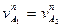Так как , а , следовательно, 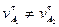, что допустимо и имеет место на практике. В процессе зацепления происходит не чистое обкатывание профилей, а соскальзывание, что приводит к износу зубьев по профилю.

Сравним треугольник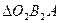и и 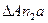. Эти треугольники подобны, поэтому очевидно равенство 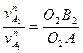, следовательно, .

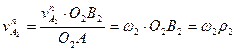Обозначим , .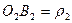

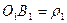Аналогично: .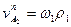

Исходя из того, что 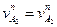, получим: .

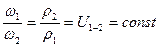Рассмотрим треугольник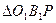и и 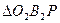. Они подобны, как прямоугольные со смежными сторонами.

Обозначим: ; .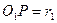

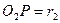Тогда: .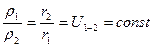

Следовательно, положение точки 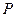на линии центров 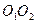в процессе зацепления должно быть неизменным.

Для постоянства передаточного отношения в зубчатой передаче необходимо, чтобы общая нормаль 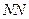к профилям зубьев всегда проходила бы через одну и ту же точку 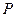(полное зацепление) на линии центров 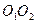, и делила бы линию центров в отношении обратно пропорциональном отношению угловых скоростей.

Следствия:

1. Чтобы в зубчатой передаче иметь постоянным передаточное отношение, необходимо профили зубьев очертить тонкими кривыми, которые отвечали бы требованиям основной теоремы зацепления.

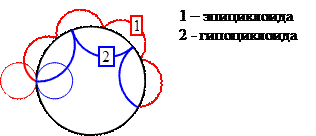
2. Требованиям основной теоремы зацепления соответствует эвольвента, образующая эвольвентное зацепление и сочетание эпициклоиды и гипоциклоиды, образующей циклоидное зацепление.

Эвольвента является бесконечной спиралью вне данной окружности.

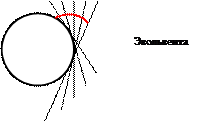Проведём обкатывание вспомогательных окружносте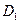й и 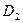без скольжения по начальной окружности, и получим эпициклоиду и гипоциклоиду.

Ножка зуба оформляется по гипоциклоиде, а головка зуба оформляется по эпициклоиде.