Понятие о геометрическом скольжении.

Примером геометрического скольжения могут служить фрикционные передачи с клинчатыми катками.

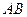Допустим, что на линии контакта есть некоторая точка 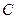, на которой скорости обоих колёс одинаковы, то есть 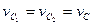. На самой линии контакта 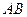, на всём её протяжении, кроме точки 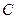, линейные скорости колёс различны, то есть 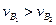и 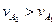. Таким образом, везде происходит относительное скольжение, что приводит к нагреву и износу сопряжённых конусных поверхностей, что, в свою очередь, понижает коэффициент полезного действия передачи. Чтобы избежать этого не следует делать общую образующую 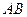больших размеров. Необходимо уметь находить оптимальный размер образующей .

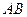Явление, где на сопряжённых поверхностях векторы линейных скоростей в одних и тех же точках различны, что связано с геометрией формы, принято называть геометрическим скольжением. Его следует избегать, однако это не всегда удаётся.

Фрикционные передачи с коническими катками.

Назначением фрикционных передач с коническими катками является преобразование вращательного движения между пересекающимися в пространстве осями.

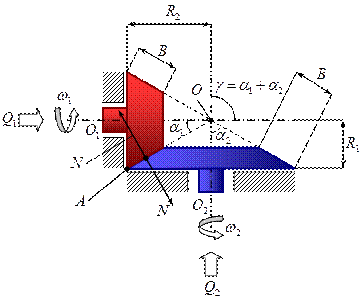
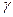- угол между осями вращения.

Передаточное отношение: .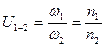

Допустим, что в некоторой точке 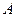выполняется услови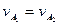е: , где 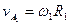, 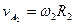. Тогда 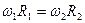или .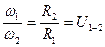

Рассмотрим два треугольника 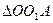и :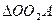

; ;

; ;

.

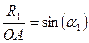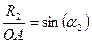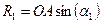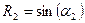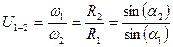Как следует из последнего выражения, передаточное отношение в передаче с коническими катками выражается через тригонометрические функции, то есть выбранное нами положение точки 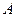на общей образующей 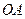безразлично, то есть на всём протяжении образующей 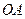в точках контакта линейные скорости одинаковы, то есть происходит чистое обкатывание без скольжения.

Это справедливо только для случая, когда общая образующая проходит через точку пересечения осей вращения катков. Если это условие нарушается, то появляется геометрическое скольжение.

Зубчатые передачи.

Зубчатые передачи – передачи, в которых усилия между колёсами передаются за счёт зацепления.

С их помощью осуществляется передача и преобразование вращательного движения между параллельными осями (цилиндрические колёса), пересекающимися осями (конические зубчатые колёса), скрещивающимися осями (цилиндрические винтовые колёса, конические колёса, гипоидная передача). Кроме того, с помощью зубчатых передач можно преобразовывать поступательное движение зубчатой рейки во вращательное движение зубчатого колеса и наоборот.

Достоинства зубчатых передач:

1. Постоянство передаточного отношения или изменение передаточного отношения по какой-либо жёсткой функции.

2. С помощью зубатых передач передаются самые большие мощности.

Недостатки зубчатых передач:

1. Сложность изготовления.

Различают зубчатые передачи с постоянным положением осей в пространстве и передачи с бегающими в пространстве осями (планетарные и дифференциальные передачи).

Геометрические параметры цилиндрических зубчатых колёс.

Ступень зубчатой передачи – два зубчатых колеса, сопряжено работающих между собой.

Начальные окружности – две окружности, которые обкатываются друг об друга без скольжения.

Начальная окружность определена только тогда, когда колёса находятся в зацеплении.

Делительная окружность – окружность, на которой толщина зуба и ширина впадины одинаковы.

На делительной окружности модуль зацепления 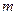есть величина стандартная.

Если передача образована нормальными, не корректированными колёсами, то начальная и делительная окружности совпадают.

Основными кинематическими параметрами зубчатых передач являются: число зубьев 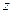и шаг зацепления 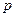- расстояние между одноимёнными точками двух соседних зубьев, измеренное по дуге делительной окружности.

Делительная окружность делит зуб на две части: на головку зуба и ножку зуба. Головка зуба 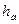находится между наружным диаметром колеса и делительной окружностью. Ножка зуба 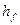находится между делительной окружностью и окружностью впадин.