Структурный анализ механизма.
Механизм – совокупность физических тел (звеньев) подвижно связанных между собой и обладающих определённостью движения. Механизм предназначен для передачи и преобразования движения.
Машина – совокупность физических тел подвижно связанных между собой и обладающих определённостью движения. Машины предназначены для преобразования одного вида энергии в другой и совершения полезной работы.
Машины бывают следующих видов:
1. Машины-двигатели, такие как электродвигатели, гидродвигатели, пневмодвигатели, двигатели внутреннего сгорания и другие.
2. Машины – орудия – машины, предназначены для совершения непосредственно технологических операций, для которых создавалась машина. Машины-орудия всегда работают в сочетании с машинами двигателями.
Все машины обязательно являются механизмами, но не все механизмы представляют собой машины.
Элементарной составной частью любого механизма является звено. Звенья бывают простые и сложные.
Простые звенья – звенья, состоящие из одной детали.
Сложные звенья – звенья, состоящие из нескольких деталей, иногда сложные звенья могут состоять из различных материалов, жёстко связанных между собой.
Подавляющее большинство звеньев – сложные звенья.
Понятия о кинематических парах и их классификация.
Два звена неподвижно связанных между собой образуют кинематическую пару. Все кинематические пары подвергаются двум независимым классификациям:
1. Пары бывают высшие или низшие:
a. Высшие пары – пары, в которых контакт осуществляется по линии.
b. Низшие пары – пары, в которых контакт осуществляется по поверхности.
2. Все пары делятся на пять классов, в зависимости от числа налагаемых связей на подвижность каждого из звеньев. Число степеней подвижности обозначается за 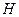 . Число налагаемых связей обозначается за
. Число налагаемых связей обозначается за 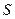 . При этом число степеней подвижности можно определить по формуле:
. При этом число степеней подвижности можно определить по формуле: 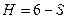 .
.
a. Пара первого класса: 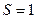 ;
; 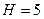 .
.
b. Пара второго класса: 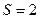 ;
; 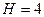 .
.
c. Пара третьего класса: 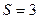 ;
;  .
.
d. Пара четвёртого класса: 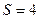 ;
; 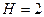 .
.
e. Пара пятого класса: 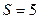 ;
; 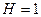 .
.


Примеры классификации пар:
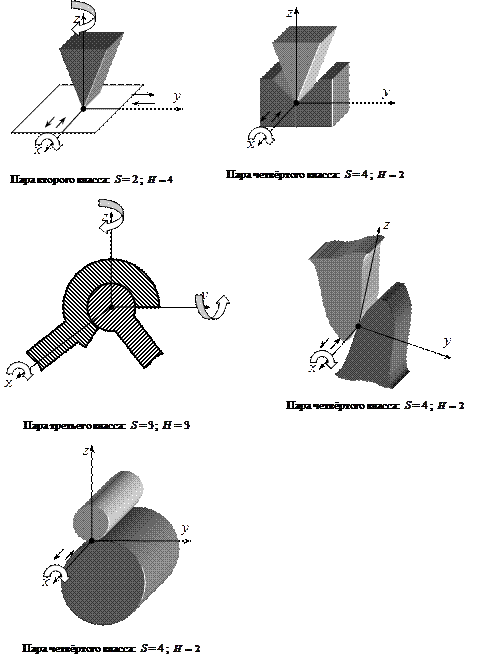
Рассмотрим кинематическую пару «винт-гайка». Число степеней подвижности этой пары 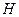 равно 1, а число налагаемых связей
равно 1, а число налагаемых связей 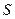 равно 5. Это пара будет являться парой пятого класса, свободным можно выбрать только один вид движения для винта или гайки, а второе движение будет сопутствующим.
равно 5. Это пара будет являться парой пятого класса, свободным можно выбрать только один вид движения для винта или гайки, а второе движение будет сопутствующим.
 Кинематическая цепь – звенья, связанные между собой кинематическими парами различных классов.
Кинематическая цепь – звенья, связанные между собой кинематическими парами различных классов.
Кинематические цепи бывают пространственными и плоскими.
Пространственные кинематические цепи – цепи, звенья которых двигаются в различных плоскостях.
Плоские кинематические цепи – цепи, звенья которых двигаются в одной или параллельных плоскостях.
Понятия о степени подвижности кинематических цепей и механизмов.
Число звеньев свободно парящих в пространстве обозначим за 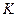 . Для
. Для 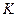 звеньев степень подвижности можно определить по формуле:
звеньев степень подвижности можно определить по формуле: 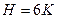 . Образуем из этих
. Образуем из этих 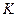 звеньев кинематическую цепь, соединив между собой звенья парами различных классов. Число пар различных классов обозначается за
звеньев кинематическую цепь, соединив между собой звенья парами различных классов. Число пар различных классов обозначается за  , где
, где 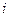 - класс, то есть:
- класс, то есть: 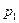 - число пар первого класса, у которого
- число пар первого класса, у которого 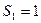 , а
, а 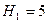 ;
; 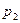 - число пар второго класса, у которого
- число пар второго класса, у которого 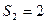 , а
, а 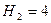 ;
; 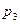 - число пар третьего класса, у которого
- число пар третьего класса, у которого 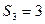 , а
, а 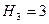 ;
; 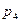 - число пар четвёртого класса, у которого
- число пар четвёртого класса, у которого 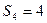 , а
, а 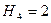 ;
; 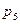 - число пар пятого класса, у которого
- число пар пятого класса, у которого 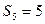 , а
, а 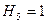 . Степень подвижности образованной кинематической цепи можно определить по формуле:
. Степень подвижности образованной кинематической цепи можно определить по формуле: 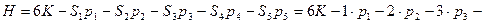
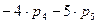 .
.
Образуем из кинематической цепи механизм. Одним из основных признаков механизма является наличие стойки (корпуса, основания), около которого движутся остальные звенья под действием ведущего звена (звеньев).
Степень подвижности механизма принято обозначать за 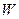 . Одно из звеньев кинематической цепи превратим в стойку, то есть отнимем у него все шесть степеней подвижности, тогда:
. Одно из звеньев кинематической цепи превратим в стойку, то есть отнимем у него все шесть степеней подвижности, тогда: 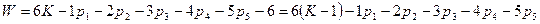 - формула Сомова-Малышева.
- формула Сомова-Малышева.
В плоской системе максимальное число степеней подвижности 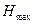 равно двум. Поэтому степень подвижности плоской кинетической цепи можно определить по следующей формуле:
равно двум. Поэтому степень подвижности плоской кинетической цепи можно определить по следующей формуле:  . Степень подвижности плоского механизма определяется по формуле Чебышева:
. Степень подвижности плоского механизма определяется по формуле Чебышева:  , где
, где 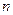 - число подвижных звеньев. Используя определение высших и низших кинематических пар формулу Чебышева можно записать следующим образом:
- число подвижных звеньев. Используя определение высших и низших кинематических пар формулу Чебышева можно записать следующим образом: 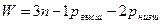 .
.
Пример определения степени подвижности:
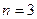
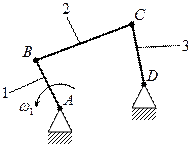 ;
;
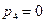 ;
;
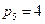 ;
;
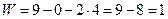 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Получение параметрических ограничений на основе анализа НИП | | | Понятие о геометрическом скольжении. |
Дата добавления: 2017-02-13; просмотров: 1053;











