Цикл теплового двигателя
Принцип преобразования тепловой энергии в механическую работу состоит в использовании эффекта значительного объемного расширения газообразных рабочих тел при их нагревании.
Чтобы реализовать этот принцип необходимо иметь машину с рабочей полостью переменного объема, который должен быть заполнен рабочим телом. Один их вариантов такой машины — цилиндр с поршнем, перемещение которого позволяет изменять рабочий объем. При подводе теплоты к газу, последний расширяется и, оказывая силовое воздействие на поршень, перемещает его и производит внешнюю работу:
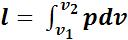 . (1.22)
. (1.22)
Из выражения (1.22) видно, что работа будет производиться только при увеличении объема рабочего тела, и как только возможности его расширения будут исчерпаны, преобразование прекратится. Для возобновления полезного действия машины, рабочее тело надо вернуть в исходное состояние, т. е. переместить поршень, уменьшив объем рабочего тела.
Таким образом, для непрерывного получения механической работы необходимо осуществить круговой процесс, т. е. цикл.
Циклом называется совокупность процессов, происходящих в определенной последовательности, в результате осуществления которых рабочее тело возвращается в первоначальное состояние.
На рис. 12 представлены р— v диаграммы циклов работы тепловых машин.
В реальных тепловых двигателях после осуществления каждого цикла происходит смена рабочего тела. Однако возможны и замкнутые циклы, совершаемые с одним и тем же рабочим телом путем изменения параметров его состояния. С точки зрения термодинамики эти две схемы совершенно эквивалентны.
При уменьшении объема рабочего тела будет происходить его сжатие с изменением параметров состояния. При этом, чем больше повышается давление и температура газа, тем выше поднимается кривая сжатия, и тем больше затраты работы на его осуществление. Возможны случаи, когда линия сжатия располагается выше или ниже линии расширения (см. рис. 12).
Очевидно, что при необходимости получения полезной работы имеют смысл только такие циклы, в которых работа сжатия lсж меньше работы расширения lp. Эти циклы называются прямыми (рис. 12, а). Они лежат в основе работы тепловых двигателей.
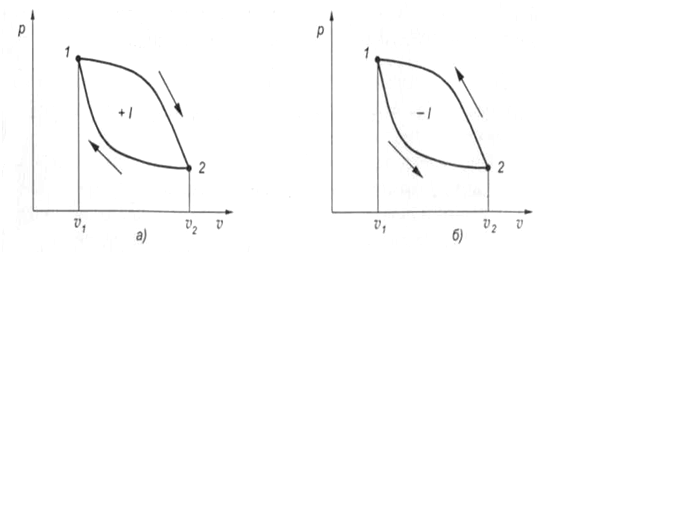
Рис. 12. Прямой (а) и обратный (б) циклы работы тепловых машин
Полезная работа прямого цикла равна разности работ расширения lр и сжатия lсж.
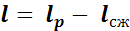 .
.
В обратных циклах
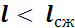 .
.
Работа обратного цикла отрицательна и используется в холодильных машинах.
Таким образом, в непрерывно действующем тепловом двигателе необходимо периодическое повторение прямых циклов, в которых процесс сжатия должен характеризоваться минимальной затратой работы.
Для выполнения последнего условия требуется, чтобы сжатие происходило при наименьшем повышении текущих значений температуры и давления, что может быть достигнуто только в случае отвода теплоты в период возвращения рабочего тела в состояние минимального объема.
Если теплоту не отводить, то работа затраченная на сжатие будет, по крайней мере, равна работе расширения и эффективность такой машины окажется равна нулю.
Таким образом, в любом случае непременным условием преобразования тепловой энергии в механическую, является прямой или косвенный расход теплоты, подведенной в цикле на возвращение рабочего тела в состояние минимального объема. Основным показателем эффективности циклов тепловых двигателей является их термический или термодинамический коэффициент полезного действия (КПД) ηt.
Термодинамический КПД определяет степень преобразования тепловой энергии в механическую в прямом цикле. Он представляет собой отношение величины тепловой энергии, преобразованной в механическую работу Аl, ко всей подведенной теплоте q1:
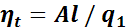 . (1.23)
. (1.23)
В соответствии с законом сохранения энергии [формула (1.4)]
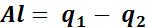 ,
,
где q2 — количество теплоты, отведенной холодильником.
Тогда
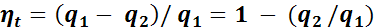 . (1.24)
. (1.24)
Цикл Карно
Одна из формулировок второго закона термодинамики звучит так: непременным условием преобразования теплоты в механическую работу является процесс передачи теплоты холодильнику. Поэтому важным вопросом является определение максимального КПД тепловых двигателей, работающих на идеальных газах.
Изучая эту проблему, французский инженер Карно в 1824 г. предложил цикл, который состоит только из обратимых процессов, совершаемый с идеальным газом. При этом Карно использовал такие процессы, которые наилучшим образом удовлетворяют своему назначению в цикле.
Знание данного цикла важно потому, что ни один из обратимых циклов не может иметь термический КПД выше термического КПД цикла Карно, осуществляемого при тех же перепадах температур.
Подвод и отвод теплоты в цикле Карно осуществляется изотермически, процессы сжатия и расширения протекают адиабатно, т. е. наиболее экономичным способом без тепловых потерь.
Двигатель, работающий по циклу Карно, представляет собой поршневую машину, цилиндр которой заполнен идеальным газом. Газ периодически контактирует с источником тепла, имеющим температуру Т1, или с холодильником, имеющим температуру Т2 (рис. 13).
Пусть газ имеет первоначальную температуру Т1 и давление р1 (точка 1). При нагревании газа от источника тепла происходит медленное изотермическое расширение (кривая 1—2) с подводом теплоты q1. После этого источник тепла удаляется и газ самопроизвольно расширяется без внешнего теплообмена (кривая 2—3) до температуры Т2 (точка 3). В процессе адиабатного расширения работа совершается за счет уменьшения внутренней энергии рабочего тела.
При осуществлении процесса расширения двигатель производит работу.
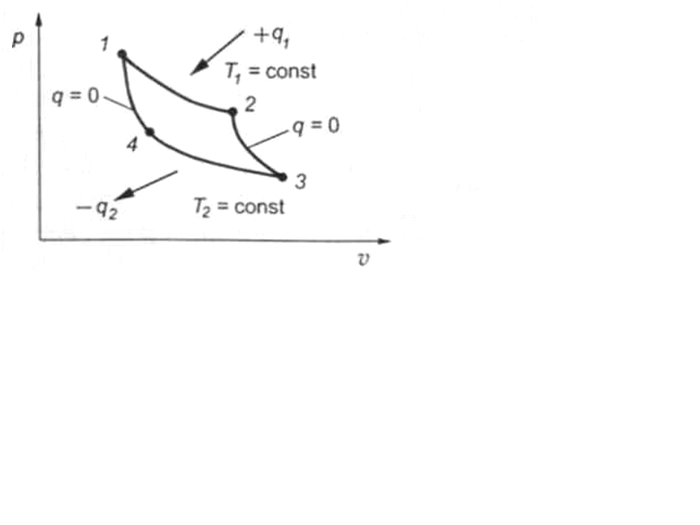
Рис. 13. р—v диаграмма цикла Карно
По окончании расширения цилиндр соприкасается с холодильником и осуществляется отвод тепла q2 в холодильник (кривая 3—4), при этом рабочее тело меняет значения своих параметров, уменьшаясь в объеме, а его давление увеличивается. Затем рабочее тело возвращается в исходное состояние путем адиабатного сжатия (кривая 4—1).
В результате цикла Карно рабочее тело совершает полезную работу, соответствующую площади, заключенной внутри контура 1—2—3—4.
Эта работа эквивалентна разности между подведенной (q1) и отведенной (q2) теплотой, т. е.
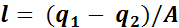 .
.
Тогда термический КПД цикла Карно на основании формул (2) и (3) можно представить как
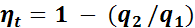 .
.
Для изотермических процессов
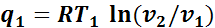 ,
,
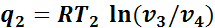 .
.
Отсюда
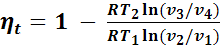 .
.
Здесь отношения объемов v3/v4 и v2/v1 равны. Тогда
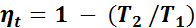 . (1.25)
. (1.25)
Дата добавления: 2017-02-13; просмотров: 7134;











