Процессы в тепловых машинах, как правило, являются политропными.

Уравнение политропного процесса:

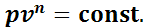(1.17)

где n — показатель политропы.

Если выразить теплоемкость газа в политропном процессе через c_n, то показатель n будет иметь вид

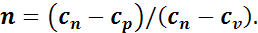
Учитывая, что с_р/с_v = k, получим

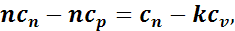
откуда

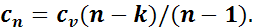
Количество теплоты определяется из уравнения первого закона термодинамики

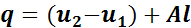
или из уравнения (3):

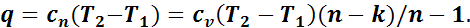(1.18)

Учитывая уравнения (1.13)—(1.17) для политропного процесса можно написать

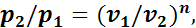(1.19)

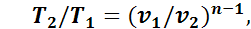(1.20)

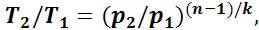(1.21)

Уравнение политропного процесса является общим для всех основных рассматриваемых процессов. Так уравнения изохорного, изобарного, изотермического и адиабатного процессов можно получить из уравнения политропного процесса, если показателю политропы n давать соответствующие значения. Например, если n = ±∞, то уравнение (1.17) примет вид v = const, что соответствует изохорному процессу, если п = 0, то vⁿ = v⁰ = 1, и уравнение (1.17) примет вид р = const, что соответствует изобарному процессу, если п = 1, то уравнение политропного процесса преобразуется в уравнение адиабатного процесса pv^k = const. Таким образом:

· для изохорного процесса n = ±∞,

· для изобарного процесса п = 0,

· для изотермического процесса п = 1,

· для адиабатного процесса п = k.

Кроме перечисленных процессов, являющимися частными случаями политропного процесса, уравнение (1.17) может выражать бесконечное число процессов, в каждом из которых показатель п будет иметь свое определенное значение, находящееся в пределе от -∞ до +∞.