Продолжение таблицы 9.4
|
| Зажимное устройство воспринимает как Р, так и МР. Расчет ведётся из условия дей- ствия Р |
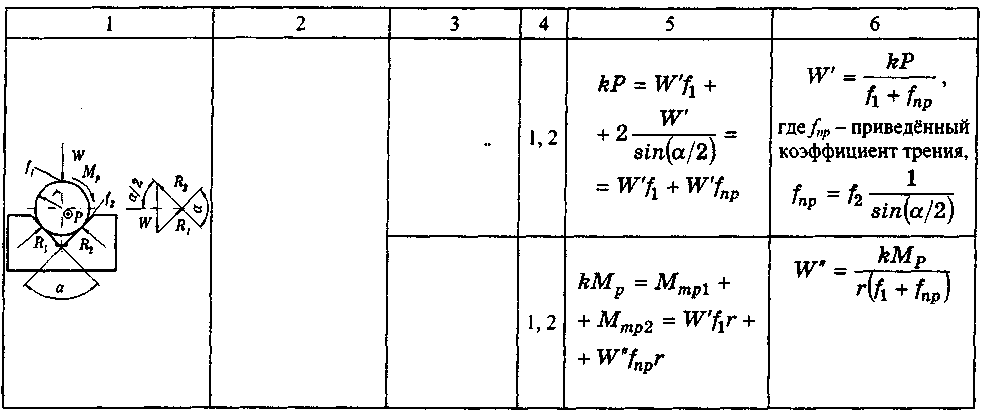
| Цилиндрическая заготовка закреп- лена в призме с углом а находится под действием момента обработ- ки МР и силы Р. Создаваемые силы и моменты трения противодействуют сдвигу вдоль оси и повороту заготов- ки |
| Расчёт из ус- ловия дейст- вия момента МР |
| За потребную силу зажима принимается большее значение из Wn W" |
При действии Мр силы Р (плечо г) заготовка может пово-
рачиваться на базовой плоскости А. Противодействуют её
повороту силы трения F (в контакте зажимного элемента с
заготовкой), Fx, F2n Fz (в контактах установочных элемен-
тов с заготовкой), которые создают моменты трения Мтр,
Мтр1, Мтр2 и Мтр3. Силы трения возникают от сил зажима
W (без учёта веса заготовки). Уравнение равновесия в дан-
ном случае 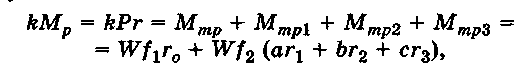 можно записать так:
можно записать так:
где а, Ъ, с — коэффициенты, показывающие части (доли)
силы W, соответствующие реакциям Rlt Д2 и R3 опор 1, 2 и 3.
Сумма коэффициентов а,Ь, с равна 1. При расположении
точки приложения силы W в центре тяжести треугольника
опор Oj коэффициенты а = Ь = с = 1/3,а реакции опор
Дх = Д2 = Д3 = W/3.
Из уравнения равновесия
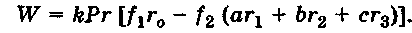
|
Следует рассмотреть также слу-
чай, когда силы обработки создают
опрокидывающие моменты, а за-
жимные устройства противодейству-
ют опрокидыванию заготовок в при-
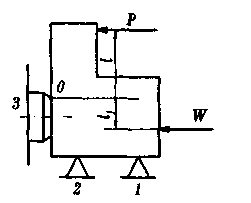
способлениях (рис. 9.3). Сила обра-
ботки Р на плече I создаёт относи-
тельно точки О опрокидывающий
момент М, сила зажима W на Рис. 9.3 Схема дей-
плече 1Х — противодействующий оп- ствия сил обработки и
рокидыванию заготовки момент зажимной силы, проти-
MnD. Подобная схема имеет место, водействующей опроки-
л. дыванию заготовки
например, при фрезеровании пазов, и~°™*»>™ *u««»uoiw*
протягивании плоских поверхностей заготовок в тисках. Рас-
положение точки приложения силы W ниже центра опорной
пластины 3 обеспечивает также надёжный контакт заготов-
ки с опорами 1 тл.2.
Условие равновесия в данном случае выражается уравне-
нием (без учёта возникающих на опорах 1, 2 сил трения)
kM= kPl = Wllr откуда
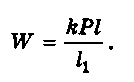
9.3 Выбор и расчёт зажимных устройств
Зажимные устройства приспособлений разделяются на
простые (элементарные) и сложные (комбинированные), со-
стоящие из нескольких простых. Простые зажимные устрой-
ства представляют собой элементарные механизмы (винто-
вые, клиновые, рычажные, эксцентриковые и т.п.); слож-
ные состоят из комбинации простых, соединённых в опреде-
лённом порядке. В зависимости от числа ведомых звеньев
зажимные устройства подразделяются на одно- и многозвен-
ные. Многозвенные устройства могут закреплять одну заго-
товку в нескольких местах или несколько заготовок в много-
местном приспособлении одновременно.
В зависимости от источника привода зажимные устрой-
ства подразделяются на ручные, механизированные и авто-
матизированные .
При расчёте зажимов приспособлений необходимо по по-
требной зажимной силе W определить основные размеры за-
жимного устройства и исходную силу (момент) для приведе-
ния его в действие. Эти задачи решаются с помощью расчё-
тов элементарных зажимных устройств.
Винтовые зажимные устройства (рис. 9.4) применяются
в приспособлениях с ручным закреплением заготовок, в ме-
ханизированных приспособлениях и на автоматических ли-
ниях в приспособлениях-спутниках. Они просты и надёжны
в работе и имеют наибольшее распространение.
При расчёте первым определяется номинальный (наруж-
ный) диаметр резьбы винта d по формуле:
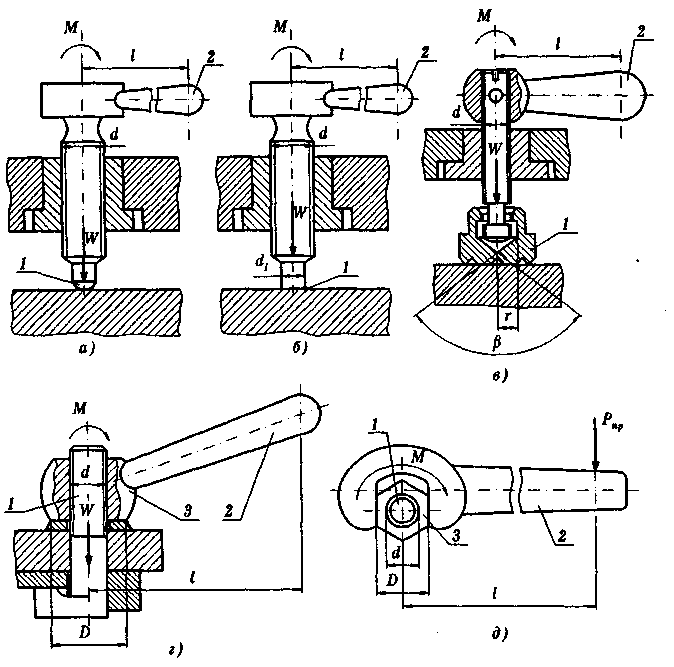
Рис. 9.4 Винтовые зажимные устройства
в виде нажимных винтов:
а — со сферическим торцом; б — с плоским торцом;
в — с башмаком (бугелем),
в виде нажимных гаек:
г — круглой формы; д — шестигранной формы;
1 — винт; 2 — рукоятка (ключ); 3 — гайка
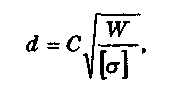
где С — коэффициент, для основной метрической резьбы
С = 1,4;
W — потребная сила зажима, Н;
[о] — допускаемое напряжение растяжения (сжатия), для
винтов из стали 45 с учётом износа резьбы можно принимать
[<т] = 80...100 МПа.
Полученное значение d округляется до ближайшего боль-
шего стандартного значения (обычно от М8 до М52).
Далее определяется момент М, который нужно развить
на винте (гайке) для обеспечения заданной зажимной силы W:
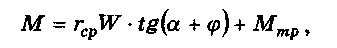
где гср — средний радиус резьбы (можно принимать rcp = 0,45tf);
а — угол подъёма резьбы (для резьб от М8 до М52 а
изменяется от 3°10' до 1°5');
Ф — угол трения в резьбе;
Мтр — момент трения на опорном торце гайки (рис. 9.4, г, д)
или в месте контакта торца нажимного винта (рис. 9.4, а, б, в):
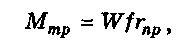
гпр — приведённый радиус кольцевого торца, для гаек
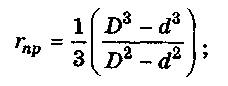
D — наружный диаметр кольцевого торца гайки.
При средних значениях а = 2°30'; <р = 10°30'; D - l,7d;
f— 0,15 можно пользоваться приближённым расчётом М для
гаек и звёздочек по формуле М = 0,2dW.
Момент открепления винтового зажимного устройства
(при <р' > а)
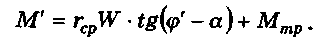
С учётом того, что при откреплении преодолевается тре-
ние покоя, <р' и Д (коэффициент трения в резьбе) следует
брать на 30...50 % большими, чем в случае закрепления за-
готовки. С учётом указанного обстоятельства и после всех
преобразований можно получить приближённую формулу для
момента открепления:
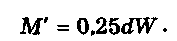
При расчёте винтовых устройств с использованием на-
жимных винтов можно использовать приведённые ниже при-
ближённые формулы расчёта момента закрепления:
для нажимного винта, показанного на рисунке 9.4, а
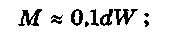
для нажимных винтов с плоским торцом (рис. 9.4, б)
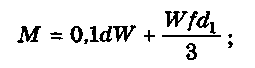
для нажимных винтов с башмаком (рис. 9.4, е)
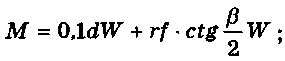
или (при р = 118 ° и / = 0,16)
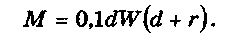
Затем выявляется длина рукоятки (ключа) I по заданной
силе воздействия из условия равновесия гайки (винта)
Рпр1 = М. Отсюда I = М/Рпр (здесь сила привода Рпр = 150 Н).
Если длина рукоятки известна, из условия равновесия на-
ходится Рпр, т.е. Рпр = М'/l, и сравнивается с силой, прикла-
дываемой рабочим или развиваемой механическим приводом.
Клиновые зажимные устройства обычно применяются в
сложных зажимных системах, но могут применяться и для
непосредственного зажима заготовок. Эти устройства просты
в изготовлении, компактны, позволяют изменять значение и
направление зажимных сил, могут обладать свойством само-
торможения. Чаще всего клиновые зажимные устройства
применяются в виде клиноплунжерных механизмов с одно-
опорными (консольными) и двухопорными плунжерами, без
роликов и с роликами; с односкосными и двухскосными кли-
ньями с опорой на поверхность корпуса и на ролики; с дву-
сторонними и круговыми (в виде конических поверхностей)
клиньями, с двумя и более консольными плунжерами с ро-
ликами и без роликов; с другими схемами устройства.
Расчёт клиновых устройств сводится к определению со-
отношения сил привода Рпр и зажима W. При известном зна-
чении Рпр обеспечиваемая клиновым механизмом сила за-
жима (на плунжере) W может определяться графически, ана-
литически и расчётом по коэффициенту усиления.
На рисунке 9.5, а изображён безроликовый клиноплун-
жерный механизм с односкосным клином 4, имеющим рабо-
чую поверхность (скос) под углом а и опирающимся на ци-
линдрическую поверхность корпуса 1, и одноопорным плун-
жером 3.
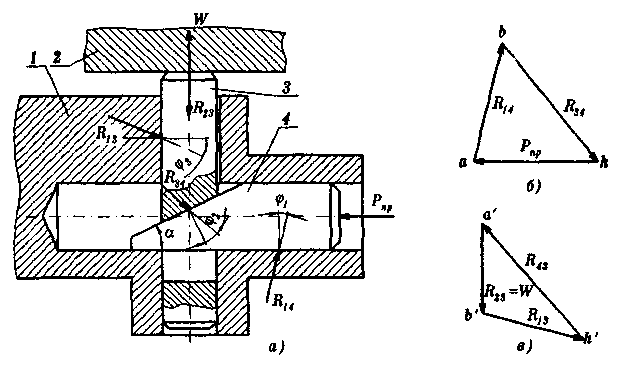
|
| Рил. 9.5 Схема клиноплунжерного механизма (а) и планы сил, действующих на клин (б) и плунжер (а) |
При графическом способе определения W по известной
силе Рпр используются векторные уравнения сил, действую-
щих на клин 4 и на плунжер 3. На клин 4, кроме силы Рпр,
действуют реакции Л34 со стороны плунжера 3 и f?14 со сто-
роны корпуса 1 устройства, которые из-за возникающих сил
трения отклонены от нормального направления на углы тре-
ния ^и^. Эти углы можно определить по коэффициентам
трения / = tgcp (<р = arctgf). При равновесии клина 4 и равен-
стве значений коэффициента трения на всех контактирую-
щих поверхностях:
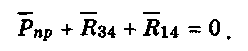
В этом уравнении известны значение и направление си-
лы Рпр, и направление сил Я34 и ^14- Поэтому оно может
быть решено графически построением плана сил (рис. 9.5, б).
Если на плане сила Рпр отложена в определённом масштабе,
то, умножив длину отрезков аЬ и bh на этот масштаб, можно
получить значение i?34 и Я14.
Теперь следует составить векторное уравнение сил для
плунжера, непосредственно зажимающего заготовку 2 (плун-
жер или толкатель клиноплунжерного механизма может дей-
ствовать и на какое-либо промежуточное звено комбиниро-
ванного зажимного устройства). На плунжер 3 действует со
стороны обрабатываемой заготовки 2 реакция Д23 (равная по
значению искомой зажимной силе W), реакция й43 со сторо-
ны клина 4 и реакция i?13 со стороны корпуса 1. Уравнение
имеет вид: 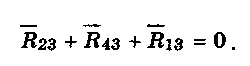
В данном уравнении также два неизвестных: сила i?23 = W
сила Д34. Значение силы it43 берётся из построенного ранее
плана сил, действующих на клин 4, так как она равна силе i?34
и направлена в противоположную сторону.
Сила Л43 откладывается от точки h (рис. 9.5, б). Через
концы вектора силы Ri3 проводятся линии, параллельные
линиям действия сил Я23 = W и ^13- В результате получают-
ся векторы искомых сил в том масштабе, в котором отложен
вектор силы R43. Так графическим путём можно найти силу W
или решить обратную задачу — по известной силе W найти
силу привода Рпр. Однако графическое определение сил тре-
бует тщательных построений и определения направления
действия сил с высокой точностью.
Из силовых многоугольников легко определить соотно-
шение сил привода Рпр и зажима W аналитически. Для од-
носкосного клина силу Рпр при заданной силе W и при пере-
даче сил под прямым углом можно найти по формуле
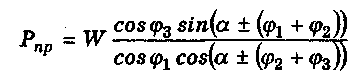
(знак плюс используется при закреплении заготовки, ми-
нус — при откреплении).
Самоторможение безроликового клина будет обеспечивать-
ся при условии а < <рх + <р2. Если <рх = <р2 = <Рз — <?■, зависи-
мость принимает вид
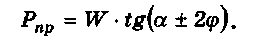
С помощью приведённой формулы легко выражается ко-
эффициент усиления ky (передаточное отношение сил):
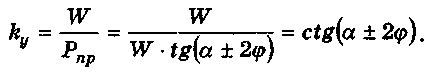
При известном коэффициенте ky можно сразу находить
значения W

Значения ky и коэффициента полезного действия (КПД)
клиноплунжерных механизмов представлены в источниках.
Рычажные зажимные устройства (рис. 9.6) чаще всего
применяются в сложных зажимных системах. С помощью
рычагов можно изменять значение и направление действия
сил, а также закреплять заготовки в двух местах или на-
правлениях.
В результате расчёта выявляются соотношения сил за-
жима W и привода Рпр. Для двухплечевого изогнутого рыча-
га с учётом сил трения его можно найти из условия (уравне-
ния) равновесия — равенства нулю суммы моментов относи-
тельно оси вращения О (рис. 9.6, а):
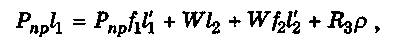
где li, l2, 1\, 12 — плечи действия сил W, Рпр и сил трения
*i = PnPh. *1 = РпрА. мм;
R3 — общая реакция оси (цапфы) рычага, направленная
из точки О'пересечения равнодействующих i?x и R2 по каса-
тельной к окружности радиусом г и определяемая из силово-
го многоугольника (рис. 9.6, б);
при равных углах трения <р : 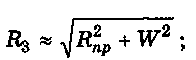
при 1г < 12: 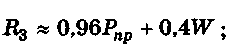
при 1Х = 12: 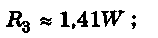
при 1г > 12. 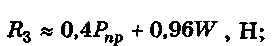
г — радиус круга трения в цапфе;
р = f'r (здесь /' — коэффициент трения в цапфе;
/'= 0,18...0,2; г — радиус цапфы), мм.
После подстановки значений R3 в уравнение равновесия
можно получить формулы расчёта Рпр по известным значе-
ниям W для различных условий:
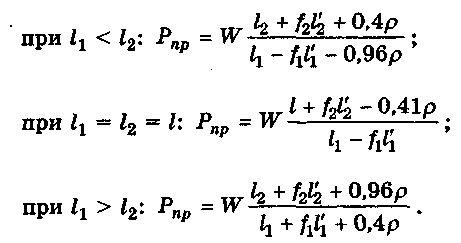
Для двухплечевых прямых рычагов (рис. 9.6, в, г) урав-
нение равновесия будет таким же, как и в предыдущем слу-
чае. После подстановки в уравнение значения
г-. 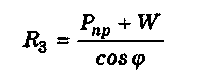
и решения его относительно Рпр получается формула расчёта
силы привода по известной силе зажима W:
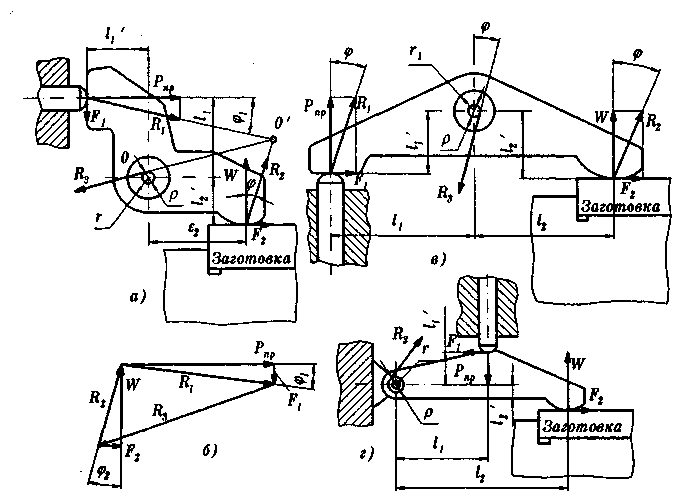
Рис. 9.6 Рычажные зажимные устройства
Дата добавления: 2021-06-28; просмотров: 573;











