Плоскопараллельное движение

Плоскопараллельным движением твердого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.

Так как положение плоской фигуры на плоскости вполне определяется положением двух ее точек или положением отрезка, соединяющего две точки этой фигуры, то движение плоской фигуры в ее плоскости можно изучать как движение прямолинейного отрезка в этой плоскости.

Предположим, что плоская фигура переместилась на плоскости из положения I в положение II. Отметим два положения отрезка АВ, принадлежащего фигуре.

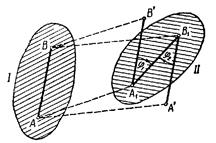
Первый вариант. Переместим фигуру поступательно, из положения АВ в положение А₁В’ т. е. так, чтобы точка А переместилась в новое положение A’ а точка В описала траекторию, тождественную траектории точки А. Затем повернем фигуру вокруг точки А’ на угол 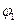так, чтобы точка В' заняла тоже свое положение B₁.

Второй вариант. Переместим фигуру поступательно из положения АВ в положение A'B₁ а затем повернем ее вокруг точки В₁ на угол 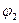так, чтобы точка А' совпала с точкой A₁.

Как видно, поступательное перемещение плоской фигуры различно в различных вариантах, а величина угла поворота и направление поворота одинаковы, т. е.

=

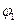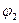
Из этого следует, что

Плоскопараллельное движение можно рассматривать как совокупность двух движений: поступательного движения плоской фигуры вместе с произвольной точкой, называемой полюсом, и поворота вокруг полюса.

При этом поступательное перемещение зависит от выбора полюса, а величина угла поворота и направление поворота от выбора полюса не зависят.

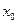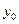Приняв за полюс некоторую точку О и обозначив и ее координаты в неподвижной системе хОу, можно определить движение полюса O а следовательно, и поступательное движение всей фигуры уравнениям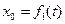и и .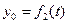

Вращательное движение фигуры относительно полюса можно описать уравнением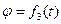

1.2.4.1 Определение скоростей точек плоской фигуры совершающей плоскопараллельное движение

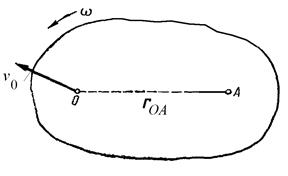
Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки вокруг полюса.

Для плоской фигуры совершающей плоскопараллельное движение в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.

Способы определения мгновенного центра скоростей

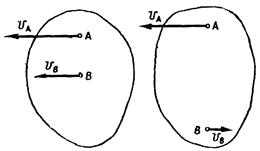
1 Если известны прямые, по которым направлены скорости двух точек плоской фигуры А и В,то мгновенный центр скоростей фигуры определится как точка пересечения перпендикуляров к этим прямым, восставленных в точках А и В.

2 Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны АВ, и известнымодули скоростей обеих точек А и В то мгновенный центр скоростей расположен на пересечении отрезка соединяющего концы векторов точек А и В с прямой АВ.

3 Если плоская фигура катится без скольжения по некоторой неподвижной кривой то ее мгновенный центр скоростей находится в точке соприкасания данной фигуры с кривой.

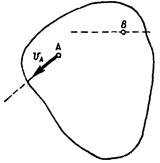
Определение скоростей точек плоской фигуры при помощи мгновенного центра скоростей

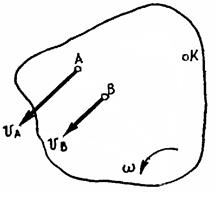
Определим скорости точек А, В и К плоской фигуры, приняв за полюс мгновенный центр скоростей Р.

Если точка Р является мгновенным центром скоростей, то 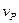=0, тогда

т. е. скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей; поэтому

Пример

Колесо радиусом R катится без скольжения по прямому рельсу. Скорость центра колеса в рассматриваемый момент времени 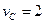м/с.

Определить скорости точек A, В_, D и Е колеса, расположенных на концах взаимно перпендикулярных диаметров.

Решение:

1-й вариант.

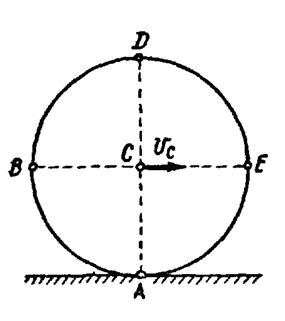
2-й вариант