Синтез алгоритмической структуры АСУ при наличии возмущающего воздействия

Если на объект действует возмущение X_В(p), которое поддается измерению, то теоретически можно синтезировать идеальную разомкнутую АСУ (рис. 7.2, б) с полной компенсацией возмущения, подав его с обратным знаком на вход регулятора с передаточной функцией (7.1).Действительно, в этом случае при X_З(p) = 0 регулируемая величина

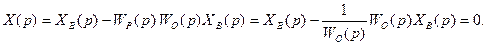(7.4)

Поэтому полезная составляющая X_У(p) на выходе объекта будет полностью уравновешивать возмущение X_В(p).

Однако возмущение X_В(p), как правило, измерить не удается, и АСУ приходится строить по замкнутой схеме (с обратной связью). Для отыскания структуры идеальной замкнутой системы можно использовать идею косвенного измерения возмущения X_В(p) с помощью модели объекта W_ОМ(p) (рис. 7.3, а). Очевидно, что при

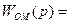W_О(p) (7.5)

вычисляемый на выходе модели объекта сигнал

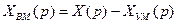(7.6)

является косвенно измеренным возмущением X_В(p) и его можно, как и в предыдыщей схеме (рис. 7.2, б), ввести в регулятор с передаточной функцией (7.1) и, таким образом, снова получить идеальную разомкнутую структуру (рис. 7.3, а). В ней в соответствии с правилами структурных преобразований сигнал W_УМ(p) можно перенести на вход регулятора и приложить к сумматору 2 (рис. 7.3, б). Тогда регулятор с передаточной функцией 1/W_О(p) окажется охваченным внутренней положительной обратной связью, а сигнал после сумматора 1 будет соответствовать сигналу ошибки

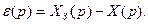(7.7)

Последнее означает, что АСУ стала замкнутой и работает по принципу отрицательной обратной связи с регулятором (см. рис. 7.3, б), имеющим передаточную функцию

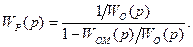(7.8)

Рис. 7.3. Алгоритмические схемы идеальной замкнутой АСУ

При точном совпадении объекта управления и его модели (W_О(p) = W_ОМ(p)) регулятор будет работать как пропорциональный с коэффициентом k_п = ¥, что соответствует нулевым ошибкам по каналам задания и возмущения.

Техническая реализация безинерционного (идеального) регулятора невозможна. Однако такая структура является идеалом, к которому необходимо стремиться при синтезировании высококачественных систем управления. В соответствии с идеальной структурой (рис. 7.3, б) можно сформулировать фундаментальный принцип структурно-параметрической оптимизации АСУ с обратной связью: регулятор должен содержать динамическое звено с передаточной функцией, равной или близкой обратной передаточной функции объекта управления.

7.3. Определение алгоритмической структуры и настроечных параметров регуляторов АСУ с инерционными статическими объектами управления

На практике наиболее часто приходится решать задачу синтеза АСУ с инерционными объектами управления с запаздыванием, которые можно описать следующей обобщенной передаточной функцией

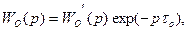(7.9)

где 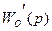- дробно-рациональная функция, характеризующая инерционную часть объекта управления; t_о – чистое запаздывание объекта управления.

Определим структуру и передаточную функцию идеального регулятора для инерционных объектов управления с запаздыванием.

Подставляя значение передаточной функции W_О(p) из выражения (7.9) в формулу (7.8) получаем передаточную функцию идеального регулятора для инерционных объектов управления с запаздыванием

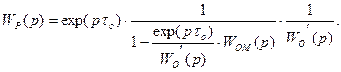(7.10)

Здесь присутствует сомножитель exp(pt_о), который соответствует идеальному упредителю и точная реализация которого технически невозможна. Поэтому с целью упрощения искомой структуры регулятора и облегчения его технической реализации полагают, что для объектов управления с чистым запаздыванием t_о , идеальная АСУ воспроизводит задающее воздействие с запаздыванием t_о , т. е.

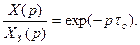(7.11)

С другой стороны, применяя правило (4.8) структурного преобразования к алгоритмической схеме АСУ (рис. 4.7), записываем отношение

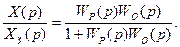(7.12)

Приравнивая правые части выражений (7.11) и (7.12) и учитывая в них значение передаточной функции W_О(p) из выражения (7.9), записываем уравнение

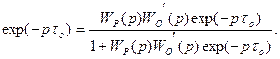(7.13)

Решая это уравнение, получаем искомую передаточную функцию идеального регулятора (регулятора Ресвика)

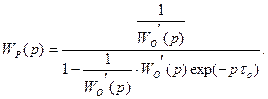(7.14)

Этой передаточной функции соответствует алгоритмическая схема АСУ (рис. 7.4), которая уже не содержит упредителя.

Рис. 7.4. Алгоритмическая схема идеальной АСУ с объектом с запаздыванием

Передаточная функция по каналу возмущения в такой АСУ согласно (4.11)

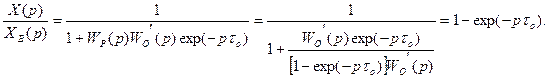(7.15)

Это означает, что действие возмущения X_В(p) мгновенно компенсируется системой через время t_о.

Ранее было показано, что инерционные статические объекты управления с s-образной переходной характеристикой (см. рис. 3.1) можно представить в виде моделей первого (3.3) или второго (3.2) порядка с запаздыванием.

Представим, первоначально, объект управления моделью первого порядка (3.3). Тогда, полагая запаздывание 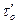модели объекта равным чистому запаздыванию t_о реального объекта и подставляя в выражение (7.14) значение передаточной функции модели (3.3), определяем передаточную функцию регулятора

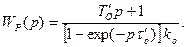(7.16)

При относительно медленно изменяющихся воздействиях можно принять

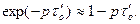(7.17)

Тогда, учитывая это равенство в выражении (7.16) получаем искомую передаточную функцию регулятора

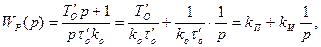(7.18)

где

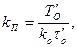(7.19)

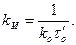(7.20)

Такую передаточную функцию имеет пропорционально-интегральный (ПИ) регулятор с настроечными параметрами k_П и k_И.

Представив объект управления более точной моделью второго порядка (3.2) и проведя аналогичные рассуждения, получаем искомую передаточную функцию регулятора

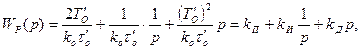(7.21)

где

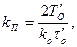(7.22)

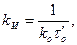(7.23)

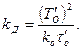(7.24)

Такую передаточную функцию имеет пропорционально-интегрально-дифференциальный (ПИД) регулятор с настроечными параметрами k_П, k_И, k_Д.

На основании полученных общих соотношений между параметрами объекта управления и регулятора можно сформулировать рекомендации по выбору типа регулятора и его настроечных параметров:

· Для объектов с запаздыванием, инерционная часть которых действительно близка звену первого порядка (а непросто аппроксимирована таким звеном!), целесообразно применять ПИ-регулятор.

· Для объектов с запаздыванием, инерционная часть которых имеет порядок n ³ 2, наилучшим регулятором является ПИД-регулятор.

Эмпирические формулы в табл. 7.1 обобщают результаты экспериментальных исследований по определению настоечных параметров типовых регуляторов для объектов с запаздыванием (при t_о / T_о = 0…1). Параметры определены путем моделирования систем при ступенчатом изменении задающего x_з воздействия. Обеспечиваемым показателем качества АСУ является перерегулирование s (0 или 20 %) на выходе объекта регулирования.

Таблица 7.1