Статистическое и геометрическое определения вероятности
Пусть в результате некоторого опыта может появиться событие А. Обозначим mn – число появления этого события в n повторениях этого опыта. Отношение
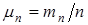 называется относительной частотой события А.
называется относительной частотой события А.
Статистическое определение вероятности. Предел 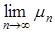 , если он существует, называется вероятностью события А :
, если он существует, называется вероятностью события А : 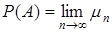 .
.
Практика показывает, что относительная частота 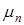 события А стабилизируется с возрастанием числа n, что гарантирует существование указанного предела.
события А стабилизируется с возрастанием числа n, что гарантирует существование указанного предела.
Недостаток классического определения вероятностей состоит в том, что оно применимо только в конечных пространствах элементарных событий и от элементарных событий требуется их “равновозможность”. Статистическое определение не требует указанных ограничений, но его теоретическая непригодность состоит в том, что невозможно точно вычислить вероятность события, поскольку относительная частота вычисляется из опытных данных.
Пример. А – “Выпал “орел” при бросании симметричной монеты”. Относительная частота этого события при большом числе подбрасывании монеты равна примерно 0,5. Статистическую вероятность этого события можно считать равной 0,5.
Пусть теперь пространство элементарных событий состоит из всех точек некоторой “измеримой” области W и выбор каждой ее точки “равновозможен”. “Равновозможность” здесь понимается в том смысле, что степень возможности выбрать точку из подмножества А Ì W пропорциональна ее мере и не зависит от ее формы и расположения. Событием называется любое “измеримое” подмножество АÌ W. Под мерой множества понимается его длина, площадь, объем в зависимости от того, является ли W подмножеством соответственно одномерного, двумерного, трехмерного пространства. Множество называется “измеримым”, если для него существует мера(т.е. длина, площадь, объем).
Геометрическое определение вероятности. Вероятностью события А называется 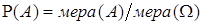 .
.
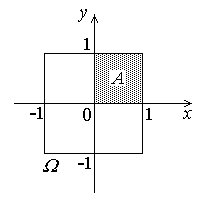 Рисунок 1.1
Рисунок 1.1
|
Геометрическое определение вероятности тоже не может служить универсальным определением вероятности, поскольку условие “равновозможности” элементарных событий сохраняется, кроме того, оно не годится в случае не “геометрических” пространств.
Пример. W – квадрат, ограниченный прямыми х = –1, х = 1, у = –1, у = 1, событие А – “выбор любой точки, лежащей в первой четверти координатной плоскости” (рис. 1.1). Тогда 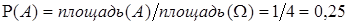 .
.
Дата добавления: 2017-02-13; просмотров: 2139;











