Эвольвента окружности и её свойства и уравнение.

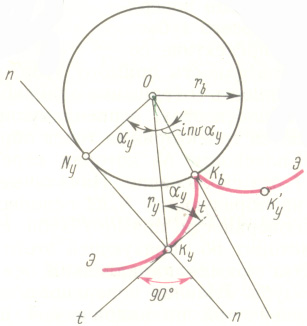Эвольвентой окружности называется кривая, описываемая любой точкой прямой линии при перекатывании её без скольжения по окружности. При этом прямая линия называется производящей прямой, а окружность – основной окружностью.

Текущий радиус-вектор точки K_y эвольвенты обозначим через r_y.

Начальный радиус-вектор этой кривой равен радиусу r_b основной окружности.

Рис 13.8

О

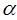Угол _y называется углом профиля.

Угол, образованный началь-ным радиус-вектором эвольвенты OK_в и её текущим радиусом OK_y называется углом развёрнутости эвольвенты или эвольвентным углом.

По построению эвольвенты имеем:

K_вN_y = K_yN_y, подставив в это выражение значение дуги и отрезка получим:

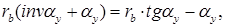откуда 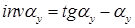(13.8)

Это уравнение выражает функциональную зависимость между углами inv 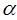_yи 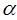_y, измеренных в радианах.

Связь между r_y, r_bи 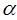_yустанавливается из 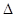K_yON_y зависимостью:

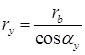(13.9)

Для геометрической теории зацепления важное значение имеют следующие свойства эвольвенты:

1. Эвольвента – симметричная кривая с двумя ветвями, сходящимися в точке K_в, которая лежит на основной окружности.

2. Эвольвента не имеет точек внутри основной окружности

3. Форма эвольвенты зависит только от радиуса основной окружности. При увеличении радиуса r_b радиус кривизны эвольвентного профиля постепенно увеличивается при r_b= 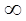эвольвента преобразуется в прямую.

4. Нормаль к любой точке эвольвенты направлена по касательной к основной окружности.

5. Центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью.