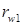Общая нормаль в контактной точке сопряжённых профилей проходит через полюс зацепления и делит линию центров на части, обратно пропорциональные угловым скоростям.
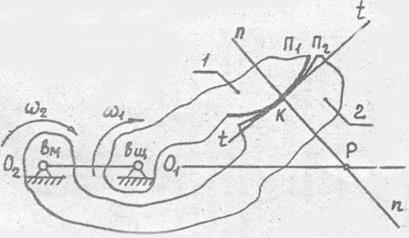
На рис. 13.6 показан общий случай взаимодействия двух плоских звеньев с произвольными, но сопряжёнными профилями. Они должны иметь общую нормаль n-n и общую касательную 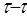 . Общая нормаль пересекает линию центров в точке P, называемой полюсом зацепления.Точку «К» можно рассматривать как две слитные точки К1 и К2, принадлежащие соответственно профилям первого и второго звеньев.
. Общая нормаль пересекает линию центров в точке P, называемой полюсом зацепления.Точку «К» можно рассматривать как две слитные точки К1 и К2, принадлежащие соответственно профилям первого и второго звеньев.

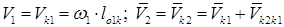 (13.1)
(13.1)
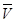 2 можно определить, используя условие существования высшей кинематической пары.
2 можно определить, используя условие существования высшей кинематической пары.
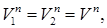
т.е. равенство проекций скоростей на общую нормаль, обеспечивающее непрерывность контакта. Проецируя V1 и V2 на общую касательную получим: V1 
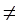 V2
V2  . Это означает что контакт профилей осуществляется со скольжением.
. Это означает что контакт профилей осуществляется со скольжением.
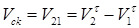 (13.2)
(13.2)
Установим связь между 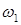 и
и 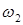 :
:
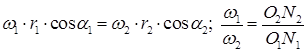 (13.3)
(13.3)
Из подобия треугольников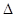 O1N1P и
O1N1P и 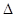 O2N2Pимеем:
O2N2Pимеем:
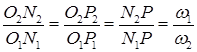 (13.4)
(13.4)
Отсюда имеем:  – эта зависимость для внешнего зацепления.
– эта зависимость для внешнего зацепления.
 У внутреннего заце-пления (рис 13.6 б) направление
У внутреннего заце-пления (рис 13.6 б) направление 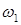 и
и 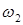 одинаковы, поэтому зависимость (13.4)имеет вид:
одинаковы, поэтому зависимость (13.4)имеет вид: 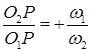
|
А в общем виде:
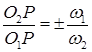 (13.5)
(13.5)
Скорость скольжения профиля.
Скорость скольжения профилей в высшей кинематической паре равна произведению скорости относительного вращения на расстояние от контактной точки до полюса зацепления:
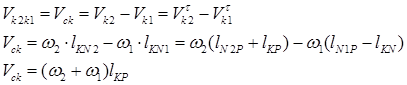 (13.6)
(13.6)
Для внутреннего зацепления 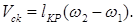
В полюсе зацепления lKP= 0и следовательно скорость скольжения равна нулюVck = 0, т.е. профили перекатываются без скольжения.
В случае цилиндрических передач рассматривают:
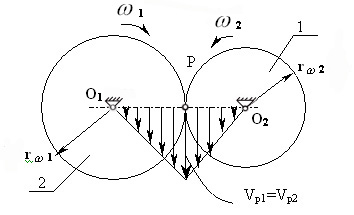
|
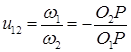
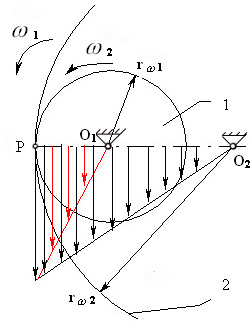
|
б) Внутреннее зацепление
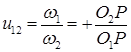
Vp = Vp1 = Vp2
|
 Vp2 = Vp1 =
Vp2 = Vp1 = 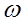 1
1  rw1
rw1
|
Ввиду ограниченности объема курса предметом дальнейшего изучения будут прямозубые и эвольвентные косозубые зубчатые передачи, у которых u = const. Геометрию таких колёс передачи определяют эвольвента окружности.
Дата добавления: 2017-02-13; просмотров: 1822;