Понятие о неуравновешинности механизма (звена)

Уравновешивание механизмов

При движении звеньев механизма в кинематических парах возникают дополнительные динамические нагрузки от сил инерции звеньев. Это возникает из-за того, что центры масс звеньев в общем случае имеют переменные по величине и направлению ускорения. Так как всякий механизм имеет неподвижное звено-стойку, то и на стойку механизма также воздействуют вполне определенные динамические нагрузки. В свою очередь через стойку эти нагрузки передаются на фундамент механизма. Динамические нагрузки, возникающие при движении механизма, являются источниками дополнительных сил трения в кинематических парах, вибраций звеньев и фундамента, дополнительных напряжений в отдельных звеньях механизма, причиной шума и т.д. Поэтому при проектировании механизма ставиться задача о рациональном подборе масс звеньев механизма, обеспечивающем полное или частичное устранение указанных динамических нагрузок. Решение подобной задачи, относящейся к динамическому проектированию механизма машины, называется его уравновешиванием.

Цель урановешивания механизмов - устранение переменных воздействий на фундамент, вызывающих кинематические колебания, как самого фундамента, так и здания, в котором он находится

Понятие о неуравновешинности механизма (звена)

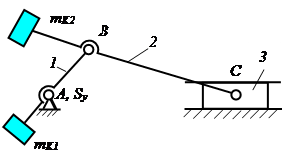
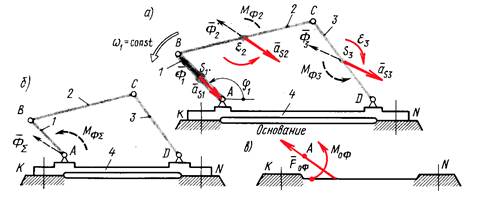
Рассмотрим плоский механизм (рис. 10.1), начальное звено 1 которого вращается с постоянной угловой скоростью. При этом все остальные звенья будут двигаться с угловыми ускорениями, а центры масс S₁, S₂, S₃ будут иметь линейные ускорения.

Рис. 10.1

Приведем всю систему сил инерции к центру А, в результате чего вся эта система сведется к общему главному вектору:

(10.1)

и к общему главному моменту: 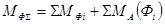, (10.2)

Т.к. w₁= соnst , то М_Ф1 = 0.

Динамические составляющие нагружения основания численно равны общему главному вектору Ф_S и общему главному моменту М_ФS системы сил инерции.

Уравновешенным считается механизм, для которого главный вектор и главный момент сил инерции равны нулю.

Если общий главный вектор сил инерции механизма Ф_S ¹ 0, то такой механизм называется статическинеуравновешенным.

Если М_ФS ¹ 0, но Ф_S = 0 - моментная неурановешенность.

Если М_ФS ¹ 0 и Ф_S ¹ 0 - динамическая неурановешенность.

Полное уравновешивание рычажных механизмов является очень трудной задачей, поэтому в большинстве случаев ограничиваются их статическим уравновешиванием. Однако и его не всегда удается осуществить в полной мере. В этих случаях производят частичное статическое уравновешивание. При статическом урвновешивании механизма необходимо обеспечить условие:

Ф_S = 0. (10.3)

Так как масса системы всех подвижных звеньев S m_i¹ 0, то ускорение центра масс S этой системы должно быть равно нулю (а_SM =0). Это условие выполняется, когда центр масс S системы подвижных звеньев механизма не перемещается. Таким образом, статическое уравновешивание есть такое действие, в результате которого центр масс системы подвижных звеньев работающего механизма становиться неподвижным.

На практике наиболее часто статическое уравновешивание проводится тремя способами:

- выбором симметричных схем механизмов;

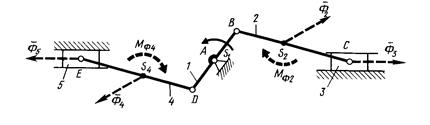
Примером такого механизма является сдвоенный кривошипно-ползунный механизм, используемый для мотоциклетных и других ДВС (рис. 10. 2).

Рис. 10. 2

Механизм выполнен кососимметричным, правая и левая шатунно-поршневые группы 2-3 и 4-5 абсолютно одинаковы, центр масс S₁ коленчатого вала находиться на оси вращения (Ф₁=0). `Ф<sub>S</sub> =`Ф₁ +`Ф<sub>2</sub> +`Ф₃ +`Ф<sub>4</sub> +`Ф₅ =0, что и свидетельствует о полной статической уравновешенности механизма.

Однако М_ФS = М_Ф2 + М_Ф4 + М_А(Ф₂) + М_А(Ф₄) ¹ 0, т.е. моментной уравновешенностью механизм не обладает.

- установкой корректирующих масс (противовесов);

Рис. 10. 3

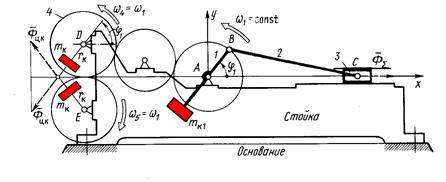
- размещением противовесов на дополнительных звеньях или кинематических цепях

Рис. 10. 4

Наиболее наглядным и простым методом уравновешивания механизмов является метод замещающих масс.