Полное статическое уравновешивание шарнирного четырехзвенника

Рис. 10. 6

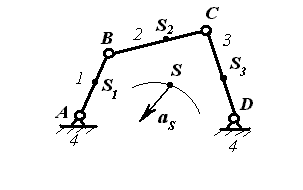
Дано: l₁, l₂, l₃

m₁, m₂, m₃

l_AS1, l_BS2, l_DS3

S₁, S₂, S₃

Определить:

m_К1, m_К3; l_К1, l_К3

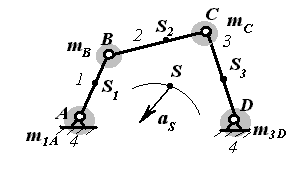
Заменим каждое звено с распределенной массой двумя сосредоточенными массами, используя систему уравнений перехода:

Рис. 10. 7

Звено 1: ; ;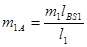

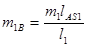Звено 2: ; ;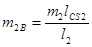

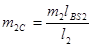Звено 3: ;;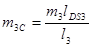

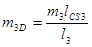
Объединим массы, размещенные в точках В и С:

m_B = m_1B + m_2B, m_C = m_2C + m_3C.

Таким образом, заданный механизм окажется заменен четырьмя массами, сосредоточенными в точках A, B, C, D. Звенья стали безинертными. Центр масс S системы остался в том же месте. При работе механизма центр масс S движется с ускорением a_S , а это означает, что заданный механизм статически неуравновешен.

Рис. 10. 8

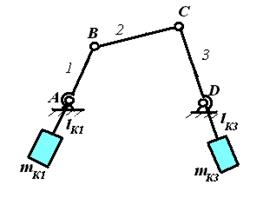
Разместим на звеньях 1 и 3 противовесы (корректирующие массы) m_К1, m_К2 с таким расчетом, чтобы центры масс систем (m_В, m_К1) и (m_С, m_К3) оказались бы в точках A и D. Для этого должны быть выполнены соотношения:

m_K1 l_K1 = m_B l₁ ; m_K3 l_K3 = m_С l₃. (10.7)

Массы противовесов m_K1 и m_K3 определяются из соотношений (10.7), если задаться размерами l_K1 и l_K3.

Докажем, что механизм стал статически уравновешенным, т.е. центр масс системы неподвижен. Объединим массы, размещенные на звеньях 1 и 3:

Рис. 10. 9

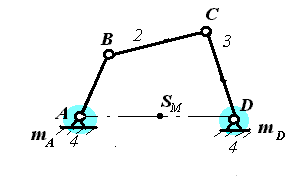
m_А = m_1А + m_В + m_К1 ;

m_D = m_3D + m_C + m_К3

Заданный механизм может быть заменен системой двух неподвижных масс m_А и m_D , поэтому центр масс этой системы и центр масс заданного механизма, но дополненного противовесами, так же станет неподвижным. А это значит, что статическое уравновешивание заданного механизма достигнуто. Центр масс уравновешенного механизма расположен на неподвижной прямой AD = l₄, и величина расстояния до центра масс 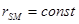может быть найдена из соотношения:

; ; .

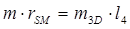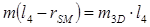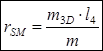Масса всего механизма m = m₁ + m₂ + m₃ + m_K1 + m_K2.