Расчет на прочность и жесткость ломаных стержней
8.1Построение эпюр внутренних усилий в раме.
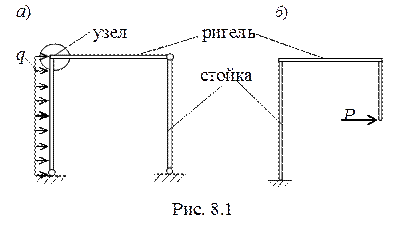
Рамой называется ломаный стержень, состоящий стоек и ригелей, соединенных жесткими или шарнирными узлами (рис. 8.1).
В плоских рамах, в отличии от балок, возникают три внутренних усилия: М – изгибающий момент, Q – поперечная сила и N – продольная сила, которые определяются методом сечений. Напомним, что изгибающий момент в сечении равен сумме моментов всех сил, приложенных к оставшейся части, относительно центра тяжести рассматриваемого сечения. Поперечная сила равна сумме проекций тех же сил на поперечную ось стержня, а продольная сила равна сумме проекций этих же сил на продольную ось стержня.
Порядок построения эпюр:
1. Определяются опорные реакции (для консольных стержней (рис. 8.1,б) можно обойтись без определения реакций).
2. Рама разбивается на участки. Границами участков служат точки приложения сосредоточенных сил или моментов, начало и конец распределенной нагрузки, узлы рамы.
3. Для каждого участка записываются выражения для внутренних усилий, производится вычисление этих усилий в пределах участка.
4. Выбирается масштаб эпюр таким образом, чтобы наибольшая ордината не превышала 1/3 ÷ 1/4 габарита рамы, и строятся эпюры M, Q, N. Эпюры Q, N строятся в одном масштабе.
5. Делается проверка построенных эпюр на соответствие приложенной нагрузки, по равновесию узлов рамы и рамы в целом.
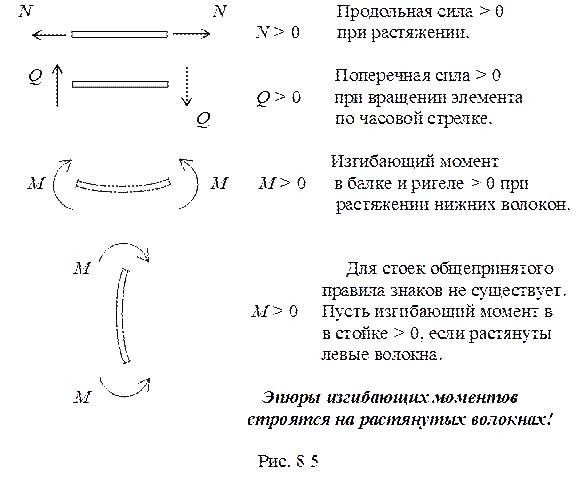
Правила знаков, применяемые при построении эпюр внутренних усилий:
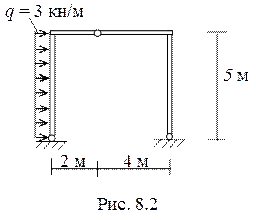
Пример 8.1 Построить эпюры внутренних усилий в трехшарнирной раме (рис. 8.2).
|
1. Обозначим в соответствии с видом опор опорные реакции (рис. 8.3) и определяем их значение, используя уравнения равновесия.
ΣmA = 0, - q··5∙2.5 + RB·6 = 0. RB = 6.25 кН.
ΣmВ = 0, - q·5·2.5 - RА·6 = 0. RА = - 6.25 кН.
Меняем направление реакции RА и считаем ее положительной (RА = 6,25кН) и направленной в низ.
Учитывая, что в шарнире С изгибающий момент отсутствует, можно записать:
ΣmCпр = 0. RB·4 - HB·5 = 0, HB = 5 кН.
ΣmCлев = 0. RА·2 + q·5·2.5 – HA·5 = 0, HA = 10 кН.
Проверка реакций.
Σх = 0. q·5 - HA - HB = 0.
Σy = 0. - RA + RB = 0.
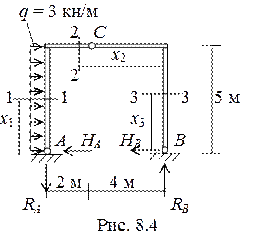
2. Обозначаем участки (рис. 8.4). В качестве «оставшейся части» оставляем ту часть рамы, к которой приложено меньше усилий.
3. Записываем выражения для внутренних усилий.
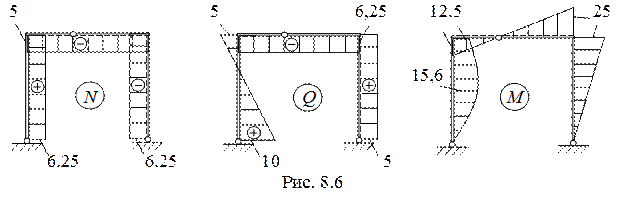
1-й участок, 0 < х1 < 5 м.
N1 = RA = 6.25 кН.
Q1 = HA - q∙x1, Qx=0 = HA = 10 кН, Qx=5 = HA = 10 - 3∙5 = - 5 кН.
М1 = - HA∙x1 + q∙x1∙x1/2. Получили уравнение квадратной параболы. Для ее построения необходимо вычислить три значения момента.
Мх =0 = 0, Мх =5 = - 10∙5 + 3∙52/2 = - 12,5 кНм,
Мх =2,5 = - 10∙2,5 + 3∙(2,5)2/2 = - 15,6 кНм.
2-й участок, 0 < х2 < 6 м.
N1 = - HB = - 5 кН.
Q1 = - RB = - 6.25 кН.
М1 = - HB∙5 + RB∙x2. Мх =0 = - 25 кНм , Мх =6 = - 25 + 6,25∙6 = 12,5 кНм,
2-й участок, 0 < х3 < 5 м.
N1 = - RB = - 6.25 кН.
Q1 = HB = 5 кН.
М1 = - HB∙x3. Мх =0 = 0, Мх =5 = - 25 кНм,
4. Строим эпюры (рис. 8.6)
|
5. Проверяем равновесие узлов. Вырежем поочередно узлы рамы с действующими в их элементах внутренними усилиями, и запишем для них уравнения равновесия (рис. 8.7). При проверке моментов пунктиром отмечены растянутые волокна.
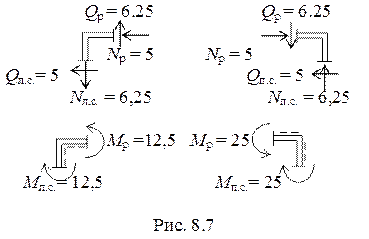
На рисунке 8.7 видно, что все уравнения равновесия (Σх = 0, Σy = 0, Σm = 0) для узлов выполняются.
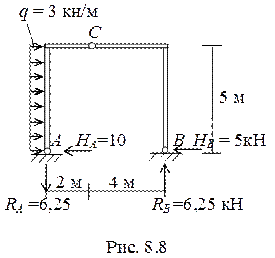
Осуществим проверку равновесия рамы в целом (рис. 8.8). Для этого восстановим значения реакций, используя эпюры внутренних усилий.
|
В точке А вертикальная реакция будет направлена вниз, поскольку левая стойка растянута, а правая реакция (т. В) направлена вверх, т. к. правая стойка сжата.
Обе горизонтальные реакции в опорах ·А и В будут направлены влево, поскольку по знаку эпюры Q (знак «+») они должны вращать элемент по часовой стрелке.
Записываем уравнения равновесия:
Σх = 0. q·5 - HA - HB = 3∙5 – 10 – 5 = 0.
Σy = 0. - RA + RB = - 6,25 + 6,25 = 0.
ΣmA = 0, - q ·5·2.5 + RB 6 = 3·5·2.5 – 6.25·6 =
= - 37.5 + 37.5 = 0.
8.2 Определение перемещений в стержневых системах
Методом Мора
Метод Мора это универсальный метод, который заключается в использовании известной теоремы Мора о равенстве возможной работы внешних и внутренних сил (7.12) и используется для определения линейных перемещений и углов поворота в любой стержневой системе от произвольной нагрузки. Метод широко применяется и при расчете статически неопределимых систем.
Пусть 1-е (грузовое) состояние представляет собой нагруженную стержневую систему заданной нагрузкой, а 2-е (единичное) состояние вызвано единичной нагрузкой Р = 1, действующей в направлении искомого перемещения. Тогда в соответствии с указанной выше теоремой получаем выражение, которое называют интегралом Мора (8.1)
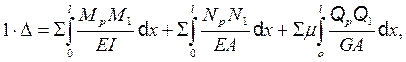 (8.1)
(8.1)
где: D ¾ искомое перемещение; Мр, Qp, Np ¾ внутренние усилия в стержневой системе, вызванные заданной внешней нагрузкой; М1, Q1, N1 ¾ внутренние усилия в стержневой системе, вызванные единичной нагрузкой, приложенной по направлению искомого перемещения в той точке (сечении), где определяется перемещение (при нахождении линейного перемещения прикладывается единичная сила Р = 1, при вычислении угла поворота прикладывается единичный момент m = 1); EI, EA, GA ¾ жесткости при изгибе, растяжении (сжатии) и сдвиге соответственно; m ¾ поправочный коэффициент, учитывающий распределение касательных напряжений в поперечном сечении; l ¾ длина участка.
Суммирование производится по всем участкам стержневой конструкции.
При расчете балок средней и большой длины и рамных конструкций влиянием продольной и поперечной сил (вторым и третьим членами формулы (4,1)) можно пренебречь в силу их малого влияния на деформации изгиба. В этом случае интеграл Мора примет вид:
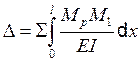 (8.2)
(8.2)
При расчете стержней, работающих только на растяжение (сжатие), и ферм в (4,1) останется только второй интеграл.
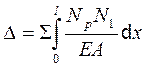 (8.3)
(8.3)
В конструкциях, испытывающих значительные поперечные силы (например, в коротких балках), необходимо учитывать влияние поперечных сил.
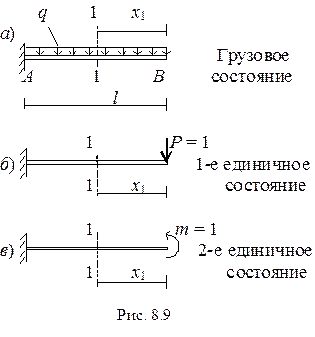
|
Пример 8.2.Вычислить прогиб и угол поворота свободного конца консоли (т. В) (рис. 8.9) от действия распределенной нагрузки.
1. В данной задаче один участок. Запишем для него выражение изгибающего момента в грузовом состоянии (рис. 8.9, а):
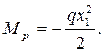
2. Для вычисления прогиба свободного конца (т. В) прикладываем в этой точке единичную силу Р = 1, т. е. создаем 1-е единичное состояние (рис. 8.9, б) и записываем выражение для единичного момента
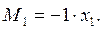
3. Записываем и вычисляем интеграл Мора, используя выражение (8.2):
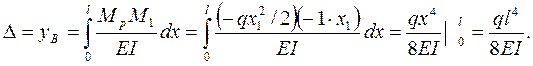
Знак «+» у D говорит о том, что перемещение происходит по направлению единичной силы Р=1.
4. Для вычисления угла поворота прикладываем в заданном сечении (т. В) единичный момент, т.е. создаем второе единичное состояние (рис. 8.9, в), и записываем выражение для единичного момента М2 на данном участке:
М2 = m = 1.
5. Вычисляем интеграл Мора при 2-м единичном нагружении:
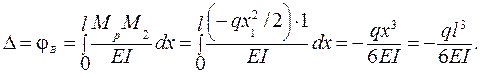
Знак «минус» говорит о том, что перемещение (поворот сечения С) происходит против направления единичного момента m = 1, т. е. по часовой стрелке.
Пример 8.3. Определить вертикальное перемещение 3 узла фермы от заданной нагрузки (рис. 8.10). Жесткость стержней ЕА = const.
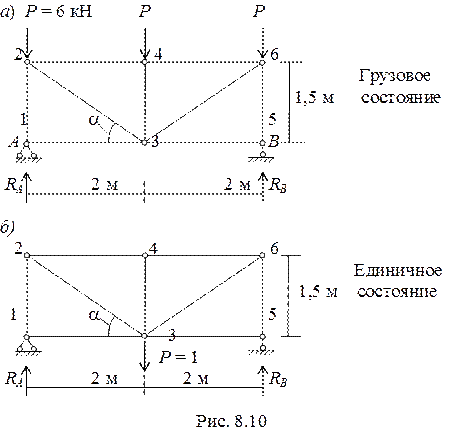
Для определения перемещений в данной стержневой системе необходимо воспользоваться формулой Мора в виде:
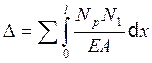 (8.3)
(8.3)
1. Определяем усилия в стержнях фермы Np от заданной нагрузки. (рис. 8.10,а). Вначале определим реакции. В силу симметрии:
RA = RB = 1.5 P= 9 кН.
Вырезая узел 1 и узел 5 можно увидеть, что

|
N12 = N56 = - 1.5 P = - 9 кН,
N13 = N35 = 0.
Вырезая узел 4, получим N34 = P.
Далее, вырежем узел 2 (рис. 8.11). (sina = 0.6, cosa = 0.8)
Sy = 0, тогда:
- P – N12 – N23sina = 0.
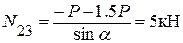 ;
;
Sx = 0, или:
N24 + N23cosa = 0. N24 = - 5∙0.8 = - 4 кН.
В силу симметрии N36 = N23 = 5 кН, N46 = N24 = - 4 кН.
2. Определяем усилия в стержнях фермы 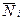 от единичной нагрузки, действующей в направлении искомого перемещения (рис 8.10,б). Определяем реакции.
от единичной нагрузки, действующей в направлении искомого перемещения (рис 8.10,б). Определяем реакции.
RA = RB = 0.5 P= 0,5.
Вырезая узел 1 и узел 5 получим
N12 = N56 = 0,5, N13 = N35 = 0.
Вырезая узел 4 получим N34 = 0.

Рассмотрим равновесие узла 2 (рис. 5.4).
Sy = 0, – N12 – N23sina = 0.
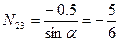 , Sx = 0, N24 + N23cosa = 0.
, Sx = 0, N24 + N23cosa = 0.
N24 = 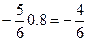 .
.
В силу симметрии N36 = N23 = 5 кН, N46 = N24 = - 4 кН.
Для вычисления по формуле (8.3) удобно полученные значения усилий свести в таблицу.
| № стержня | Np (кН) | 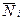
| li | Np∙ 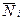 ∙li ∙li
|
| 1-2 | - 9 | - 0,5 | 1.5 | 6,75 |
| 1-3 | ||||
| 2-3 | 5/6 | 2.5 | 10.42 | |
| 2-4 | - 4 | - 4/6 | 5.33 | |
| 3-4 | - 6 | 1.5 | ||
| 3-5 | ||||
| 3-6 | 5/6 | 2.5 | 10.42 | |
| 4-6 | - 4 | - 4/6 | 5.33 | |
| 5-6 | - 9 | - 0,5 | 1.5 | 6,75 |
| S | 45.01 |
Таким образом, узел 3 опускается вниз на величину D3 = 45.01/EA.
Обычно, в зависимости от нагрузки и условий опирания, стержневую систему приходится разбивать на несколько участков, и интегрирование по формуле (8.2) необходимо проводить на каждом участке, что становится весьма трудоемким. В этом случае удобно использовать правило Верещагина для вычисления интеграла Мора (8.4).
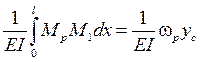 . (8,4)
. (8,4)
Оно заключается в следующем: если построить грузовую и единичную эпюры Мр и М1 (рис. 8,13) , то результат их «перемножения» (вычисления интеграла) на отдельном участке равен произведению площади грузовой эпюры wp на ординату единичной эпюры ус, взятую под центром тяжести площади грузовой эпюры. При выводе этой формулы было учтено, что единичная эпюра всегда линейна.
Действительно, при EI = const интеграл S можно представить как (рис. 8.13)
S = 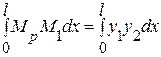 .
.
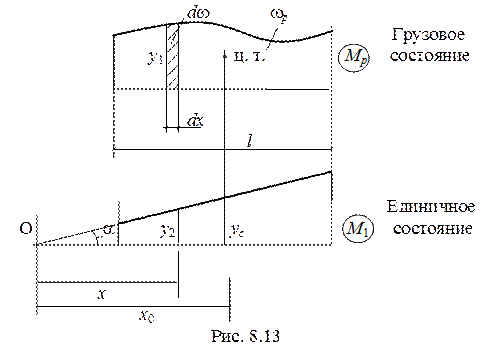
Ординату у2 можно выразить через абсциссу х: у2 = х∙tga,
тогда
S = 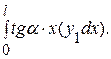 .
.
Учитывая, что 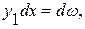 можно записать
можно записать
S = 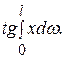
Интеграл 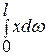 - статический момент площади эпюры Мр относительно точки О и равен площади этой эпюры, умноженной на координату х0, т. е.
- статический момент площади эпюры Мр относительно точки О и равен площади этой эпюры, умноженной на координату х0, т. е.
S = tgα∙wр∙x0.
В свою очередь, х0tga = yc. Следовательно, интеграл S равен
S = w∙ус
Рассмотренное выше правило перемножения эпюр было дано А. Верещагиным в 1925 г.
В том случае, когда обе эпюры прямолинейны (рис. 8.14) формулу (8.2) можно представить в виде
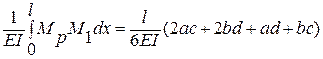 . (8.5)
. (8.5)
Формула (8.5) получена еще в 1905 г. Мюллером-Бреслау.
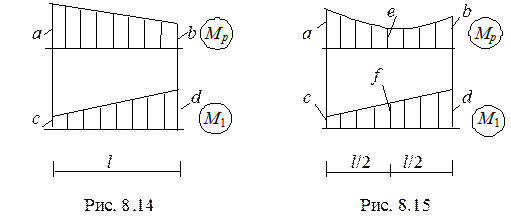
В тех случаях, когда определение положения центра тяжести и площади грузовой эпюры приводит к громоздким вычислениям, проще для «перемножения» эпюр воспользоваться формулой Симпсона (8.6):
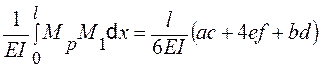 , (8.6)
, (8.6)
здесь a, b, c, d ¾ ординаты на грузовой и единичной эпюрах в начале и конце участка длиной l (рис. 8,15); e, f ¾ ординаты в середине участка.
Покажем примеры применения формул графического интегрирования Верещагина (8.4) и Симпсона (8.6).
Пример 8.4Для заданной балки (рис. 8.16,а) вычислить прогиб в сечении C и угол поворота сечения В. При определении деформаций воспользоваться методом Мора.

Для вычисления заданных деформаций необходимо построить эпюры изгибающих моментов в грузовом Мр и единичных М1 и М2 состояниях.
1. Рассматриваем грузовое состояние. Запишем выражение для Мр
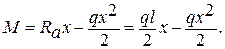
Mx=0 = 0, 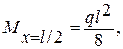
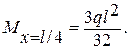
Эпюра Мр показана на рис. 8.16, б.
2. Создаем 1-е единичное состояние - прикладываем в сечении С единичную силу (рис. 8.16,в) и строим первую единичную эпюру М1 (рис. 8.16,г).
3. Для определения прогиба в сечении С перемножаем эпюры Мр и М1 по правилу Симпсона (8,6). Поскольку единичная эпюра имеет два участка перемножение эпюр производим на каждом участке ( в силу симметрии эпюр результат умножаем на 2).
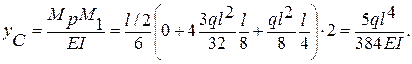
4. Создаем 2-е единичное состояние - прикладываем в сечении В единичный момент (рис. 8.16,д) и строим вторую единичную эпюру М2 (рис. 8.16,е).
5. Перемножаем эпюры Мр и М2
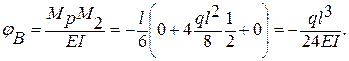
При перемножении поставлен знак минус, поскольку ординаты грузовой и второй единичной эпюр отложены в разные стороны. Минус у перемещения означает, что поворот сечения В происходит в направлении, обратном направлению единичного момента, т. е. против часовой стрелки.
Пример 8.5Для заданной балки (рис. 4.17,а) вычислить прогибы в сечениях С и D, показать вид изогнутой линии. При определении деформаций воспользоваться методом Мора.
Для определения деформаций в заданных сечениях необходимо построить грузовую эпюру М от заданной нагрузки Р и q, а также единичные эпюры Мi, полученные от воздействия на балку соответствующих единичных нагрузок Рi.
Не останавливаясь на порядке построения грузовых эпюр М и Q, покажем их в окончательном виде (рис. 4.17,б). Для построения единичных эпюр создаем единичные состояния (заданная балка нагружается только соответствующей единичной силой, приложенной в том сечении, в котором определяется перемещение). В соответствии с правилами строим эпюры М1 от силы Р1=1, приложенной в точке С, и М2 от силы Р2=1, приложенной в точке D. На рисунке единичные состояния и соответствующие единичные эпюры совмещены (рис. 4.17,в и г).
Перемножение эпюр производим по правилу Симпсона:
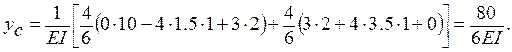
При вычислении уd перемножение эпюр на участке DА производим по правилу Верещагина (4.4), на участке АВ ¾ по формуле Симпсона (4.6).
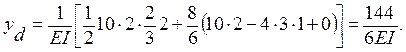
На рисунке рис. 8.17,д показана изогнутая ось балки, соответствующая вычисленным перемещениям и эпюре Мр.

Пример 8.6Вычислить горизонтальное перемещение узла D в трехшарнирной раме постоянной жесткости (рис. 8.18,а). Воспользуемся методом Мора.
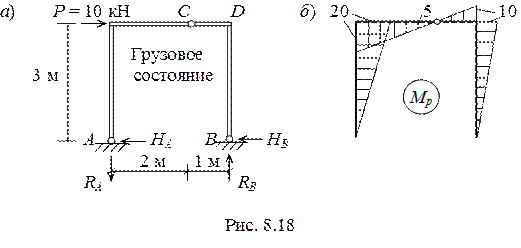
|
1. Строим грузовую эпюру Мр для грузового состояния(рис. 8.18,б). Вначале необходимо определить опорные реакции, для чего записываем соответствующие уравнения равновесия.
SmA = 0, - P∙3 + RB∙3 = 0, RB = 10 кН.
SmСпр= 0, - НВ∙3 + RB∙1 = 0, НB = 10/3 кН.
SmВ = 0, - P∙3 + RА∙3 = 0, RА = 10 кН.
SmСлев = 0, - НА∙3 + RА∙2 = 0, НА = 20/3 кН.
Проверка: Sх = 0.
При построении эпюры Мр используем методику построения эпюр в ломаном стержне
2. Строим единичную эпюру моментов М1 от действия горизонтальной единичной силы, приложенной в узле D (рис. 8.19,а ).
SmA = 0, - P∙3 + RB∙3 = 0, RB = 1.
SmСпр= 0, - НВ∙3 + RB∙1 = 0, НB = 1/3 кН.
SmВ = 0, - P∙3 + RА∙3 = 0, RА = 1 кН.
SmСлев = 0, - НА∙3 + RА∙2 = 0, НА = 2/3 кН.
Эпюра М1 показана на рис. 8.18,б.
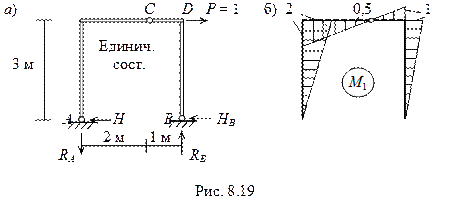
|
В связи с простым очертанием эпюр Мр и М1 перемножение эпюр на стойках производим по правилу Верещагина, а в ригеле по правилу Симпсона
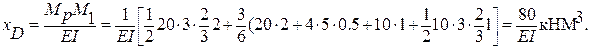
Если принять, что жесткость ригеля больше жесткости стоек (пусть EIр = 4EIст ), то:
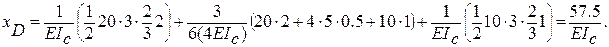
Увеличение жесткости ригеля в 4 раза привело к уменьшению перемещения узла D на 28,3%.
Представленные выше примеры показывают, что метод Мора достаточно прост для определения перемещений в заданных сечениях в любых стержневых системах.
9 Список рекомендуемой литературы
1. Саргсян А. Е. и др. Строительная механика. М.: Высш. шк., 2000. 416 с.
2. Дарков А. В., Шапошников Н. Н. Строительная механика. М.: Высш. шк., 2010. 607 с.
3. Смирнов А. В., Иванов С. А., Тихонов М. А. Строительная механика. М.: Стройиздат, 1984. 210 с.
4.Снитко Н. К. Строительная механика. М. Высш. шк. 1972. 488 с.
5. Киселев В. А. Строительная механика. Общий курс. М.: Стройиздат, 1986. 520 с.
6. Леонтьев Н. Н., Соболев Д. Н., Амосов А. А. Основы строительной механики стержневых систем. М.: Изд. АСВ, 1996. 541 с.
7. Варданян Г. С. и др. Сопротивление материалов с основами теории упругости и пластичности. М.: Изд. АСВ, 1995. 572 с.
8. Сесюнин Н. А. и .др. Примеры решения типовых задач по строительной механике. Методические указания. М., Изд. МГОУ, 1993, 116 с.
Дата добавления: 2017-02-13; просмотров: 4018;











