Основные теоремы строительной механики

При деформировании упругого тела точки его, в том числе и точки приложения нагрузки, получают перемещения. Произведение силы на путь, пройденный точкой приложения силы, будет равен работе этой силы. Т. е. при деформировании внешние силы совершают работу.

Введем понятия об обобщенной силе и обобщенном перемещении, которые позволят нам дальнейшие выводы делать в более общей и компактной форме. Под обобщенной силой будем понимать не только сосредоточенную силу, но и группы сил (момент, распределенную нагрузку, систему сосредоточенных грузов) и обозначать буквой Р.

Каждой обобщенной силе соответствует определенный тип обобщенного перемещения D. Это соответствие заключается в том, что произведение обобщенной силы на обобщенное перемещение равно работе PD (рис. 7.1).

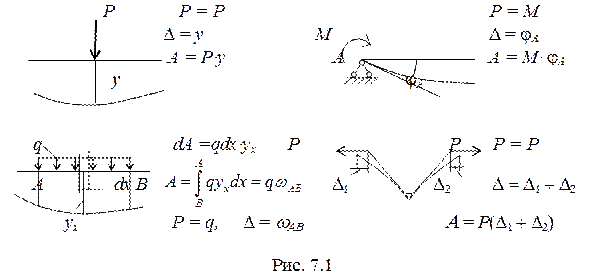
Обобщенная сила и обобщенное перемещение подчиняются закону Гука.

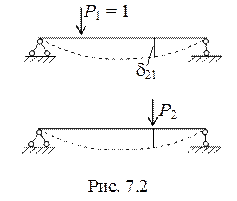
Перемещение от единичного воздействия будем обозначать d_mn. Так (рис. 7.2) единичное перемещение d₂₁ представляет собой перемещение по направлению второй силы Р₂ , вызванное действием на упругую системы единичной силы P₁ = 1.

Если вместо силы P₁ = 1 на систему будет действовать в том же направлении другая сила Р ≠ 1, то можно записать

D₂₁ = Р∙ d₂₁.

При действии на линейно деформируемую систему (подчиняющуюся закону Гука) системы n сил Р₁, Р₂, …P_n, полное перемещение по направлению m будет равно

D_mp = P₁d_m1 + P₂d_m2 …… P_nd_mn (7.1)

Выражение (1) носит название принцип независимости действия сил. Он справедлив, когда перемещения малы по сравнению с генеральными размерами тела, а возникающие в теле напряжения меньше предела пропорциональности s_пр (т. е. не должно быть остаточных деформаций).

В соответствии с (1) для системы, показанной на рис. 7.3 можно записать

7.2Работа внешних сил.

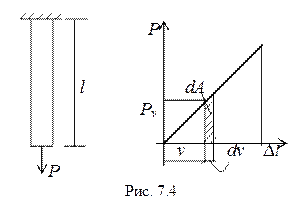
Необходимо определить работу силы Р (рис. 7.4) при статическом воздействии. График работы представлен там же.

Элементарная работа силы P_v составит dA = P_vdv. Полная работа будет

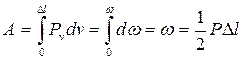(7.2)

Выражение (7.2) для действительной работы носит название теорема Клайперона (1852 г.). Действительная работа внешней силы это работа, совершаемая на перемещениях, вызванных самой силой.

Запишем выражение (7.2) в следующем виде

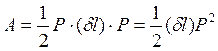. (7.3)

где 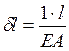- перемещение, вызываемое единичной силой.

Таким образом, работа внешней силы является квадратичной функцией и всегда положительна. Для нее не применим принцип независимости действия сил.

Кроме действительной может быть и возможная работа – это работа на перемещении, вызываемым другой силой.

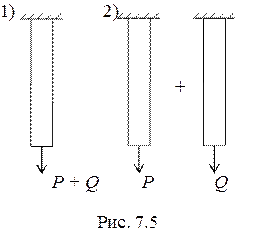
Рассмотрим два варианта приложения нагрузки (рис. 7.5). Вначале нагрузим стержень сразу двумя силами P и Q. Работа этой системы сил будет

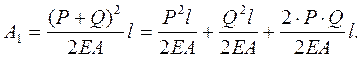
Теперь нагрузим стержень отдельно силой Р, и силой Q

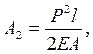
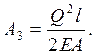
Видно, что А₁ ≠ А₂ + А₃. Разность 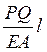представляет собой возможную работу. График такой работы представлен прямой, параллельной оси абсцисс.

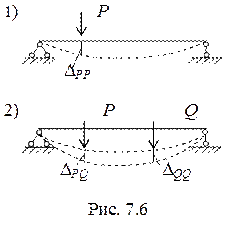
Рассмотрим более общий случай нагружения. Вначале прикладываем силу Р, затем добавляем силу Q (рис. 7.6). Тогда работа внешних сил будет равна

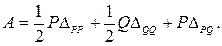
Первые два слагаемых представляют собой действительную работу сил Р и Q, а последний - возможную работу силы Р, на перемещениях, вызываемых силой Q.

Теперь вначале приложим силу Q , затем силу Р

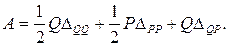
Тогда следует, что:

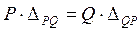или

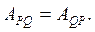(7.4)

Выражение (7.4) – теорема о взаимности возможных работ, Таким образом, в линейно-деформируемой системе возможная работа внешних (или внутренних) сил состояния 1 на перемещениях состояния 2 равна возможной работе внешних (или внутренних) сил состояния 2 на перемещениях состояния 1. Этот вывод и носит название теоремы взаимности работ, или теоремы Бетти.

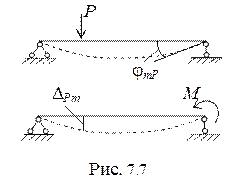
Теорему Бетти можно проиллюстрировать следующим примером (рис. 7.7).

P∙D_Pm = M∙j_mP

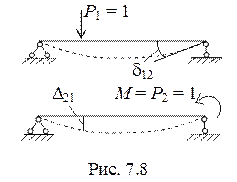
Если в предыдущих примерах допустить, что на упругую систему действуют единичные усилия P_i = 1, то они будут вызывать соответствующие единичные перемещения d_ij. Тогда из теоремы Бетти следует

d₁₂ = d₂₁. (7.5)

Выражение (7.5) представляет собой теорему о взаимности перемещений, доказанную Максвеллом в 1864 г. Оно трактуется следующим образом: единичное перемещение в 1-м направлении, вызванное единичной силой, приложенной во 2-м направлении равно единичному перемещению во 2-м направлении от действия единичной силы по 1-му направлению.

Размерность единичного перемещения

d_ij =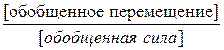

Действительно (рис. 7.7):

d₁₂ = 1/ кН, d₂₁ = м/кНм = 1/кН.

Теорема Максвелла позволяет

1. вносить значительные упрощения при расчете статически неопределимых задач,

2. строить линии влияния перемещений как эпюры.

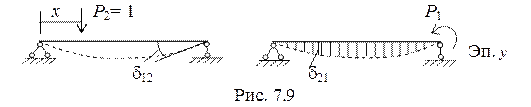
Пусть стоит задача построить линию влияния d₁₂ от подвижной силы Р = 1. На основании теоремы (7.5) можем заменить построение линии влияния d₁₂ построением эпюры d₂₁. Т. е задачу построения линии влияния угла поворота на правой опоре (рис. 7.9) можно заменить построением эпюры прогибов от действия на правой опоре единичного момента.

7.3Работа внутренних сил

В процессе нагружения упругой системы работу совершают не только внешние, но и внутренние силы, которые развиваются во всех деформируемых элементах. Поскольку в упругой системе не происходит потерь энергии на преодоление трения, выделения тепла и т. п., действительная работа внешних сил A равна и противоположна по знаку действительной работе внутренних сил W, что является выражением закона сохранения энергии:

A + W = 0или

A = - W. (7.6)

Можно сказать, что работа, произведенная внешними силами, накапливается (аккумулируется) в упругом теле в виде энергии деформаций. Поэтому работа внутренних сил W, взятая с обратным знаком и характеризующая эту энергию, носит название потенциальной энергии деформаций упругой системы U.

U = A = - W. (7.7)