Кинематический анализ сооружений
2.1 Понятие о геометрической неизменяемости
Любую расчетную систему сооружения можно представить в виде геометрически неизменяемой системы плоских тел, расположены в одной плоскости, соединенных между собой шарнирами и прикрепленных к земле при помощи опорных устройств.
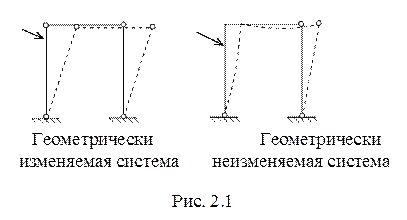
Под геометрически неизменяемой системой понимается такая система соединенных между собой тел, которая не допускает взаимного перемещения ее частей без их деформаций (рис. 2.1).
Задача кинематического анализа и состоит в том, чтобы определить геометрически изменяема или неизменяема данная система. Он проводимого в два этапа. Вначале определяется степень статической неопределимости конструкции, т. е. наличие или отсутствие лишних внешних или внутренних связей. Затем проводится собственно кинематический анализ образования (создания) конструкции, который заключается в исследовании взаимного расположения элементов конструкции (дисков) и соединяющих их связей.
2.2 Степень свободы кинематической цепи, составленной из дисков
Степенью свободы какого-либо тела или системы называется количество независимых геометрических параметров, определяющих положение тела или системы.
|
Будем рассматривать плоское движение (перемещение). Если имеем движущуюся точку, то положение ее в плоской системе координат определяется двумя ее координатами х и у.
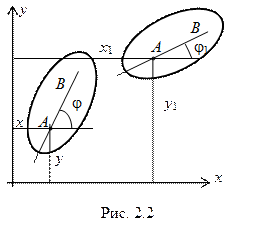
Если имеем какое-либо тело, то его положение в плоскости уже определяется тремя параметрами х у и j (рис. 21.2), т. е. мы говорим, что тело в плоскости имеет три степени свободы W = 3.
Степень свободы может быть уменьшена какими-либо препятствиями. Всякое устройство, уничтожающее одну степень свободы будем рассматривать как одну кинематическую связь. Если одно устройство уничтожает несколько степеней свободы, то оно рассматривается как соответствующее количество кинематических связей.
Цилиндрический шарнир с неподвижной геометрической осью накладывает две связи. Если мы закрепим наше тело при помощи такого шарнира в точке А, то оно уже не будет иметь возможности перемещаться поступательно и его положение будет определяться только одним параметром углом j.
Расчетные схемы сооружений имеют вид кинематических цепей, состоящих из геометрически неизменяемых элементов (дисков), соединенных между собой шарнирами и прикрепленных к неподвижному элементу (земле) опорными стержнями.
Степень свободы такого сооружения можно определить следующим образом - каждый диск обладает тремя степенями свободы. Следовательно, если бы диски не были связаны между собой и с землей, то степень свободы определялась бы как 3∙Д, где Д – число дисков. Далее, каждый шарнир, соединяющий два диска между собой, накладывает две связи и каждый опорный стержень накладывает по одной связи. Следовательно, за счет шарниров и опорных стержней степень свободы уменьшается на 2∙Ш + С0 и будет равна
W = 3Д- 2Ш - C0, (2.1)
где W - степень свободы; Д - число жестких дисков, из которых состоит данная конструкция; Ш - число одинарных шарниров; С0 - число опорных стержней.
Если W > 0, то данная конструкция изменяема, подвижна, т. е. является механизмом и не обеспечивает восприятие заданной на нее нагрузки, если W = 0 или W < 0, то такая конструкция может быть неизменяемой. В последнем случае, когда степень свободы W отрицательна, заданная система имеет лишние связи и является статически неопределимой.
Если рассматривается система не связанная с землей, так называемая свободная система, то ее степень свободы может быть определена как
W = 3Д- 2Ш - 3. (2.2)
Количество лишних связей системы определяется количеством степеней свободы W с обратным знаком.
Под одинарным шарниром понимается шарнир, соединяющий два элемента (диска) в данной конструкции. Если шарнир соединяет одновременно три диска, то он называется двойным, т. е. выполняет функции двух одинарных шарниров, и т. д.
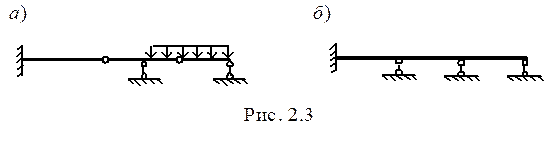
Определим степень свободы многопролетной балки (рис. 2.3, а), которая образована из трех простых балок, соединенных двумя одинарными шарнирами и имеющей 5 опорных связей:
W = 3D - 2Ш – С0 = 3×3 - 2×2 - 5 = 9 – 9 = 0.
Многопролетная балка (рис. 1.3, б) образована из одной протяженной балки с шестью опорными связями. Подсчитаем ее степень свободы:
W = 3D - 2Ш - С0 = 3×1 - 2×0 - 6 = - 3.
То есть, эта многопролетная неразрезная балка трижды статически неопределима или, другими словами, имеет три лишние связи.
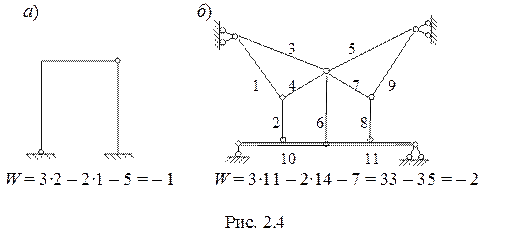
Рама, показанная на рисунке 2.4, а состоит из двух дисков, одного одинарного шарнира и пяти опорных связей (3 в защемлении и 2 в шарнирной неподвижной опоре). Степень свободы ее W = -1 (имеет одну лишнюю связь). Комбинированная система , показанная на рис. 2.4,б имеет две лишних связи.
2,3 Степень свободы шарнирно-стержневой плоской системы
|
Для шарнирно-стержневых систем применима и другая формула для определения степени свободы.
Шарниры, соединяющие звенья такой системы (рис. 2.5), можно рассматривать как точки (узлы), имеющие по две степени свободы каждая. Следовательно, суммарная степень свободы равна 2∙У. Шарниры, соединены стержнями, которые накладывают каждый по одной связи, т. к. они сохраняют постоянное расстояние между ними. Полное число связей будет 2∙У - С.
Получаем следующую формулу:
W = 2∙У – С - Со, (2.3)
Здесь: У - число узлов фермы; С - число стержней фермы; С0 - число опорных связей.
Для свободной системы
W = 2∙У – С – 3. (2.4)
В качестве примера предлагается определим степень свободы стержневых систем, представленных на рисунке 2.6.
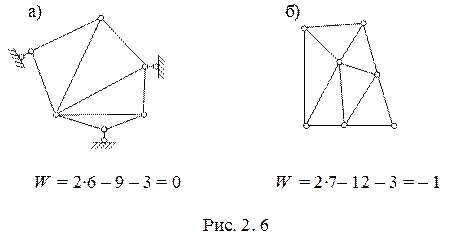
2.4 Принципы образования геометрически неизменяемых
Плоских систем
Условие W ≤ 0 не является достаточным признаком того, что система геометрически неизменяема. Это только необходимое условие, поскольку при W ≤ 0 система может быть изменяемой (рис. 2.7, рис.2.8).
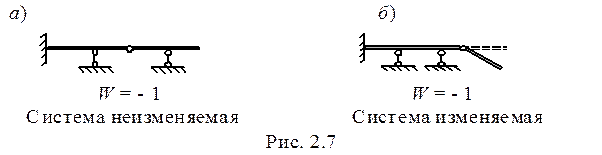
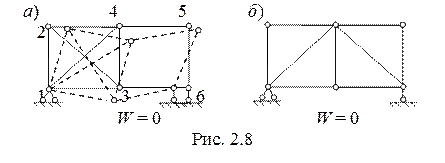
Проведем кинематический анализ простейшей фермы (рис. 2.8, а), имеющей, как и простая балка, три связи с землей. Цифрами обозначены узлы фермы.
1. Определяем степень свободы
W = 2У - C - C0 = 2×6 - 9 - 3 = 0,
т. е. данная ферма не имеет лишних связей (стержней) и может быть неизменяемой.
2. Анализируя расположение стержней в предложенной стержневой системе, видим, что левая панель, образующая жесткий диск, а правая часть данной фермы представляет собой изменяемый шарнирный четырехугольник. То есть предложенная схема стержневой конструкции изменяема. Если перенести один из стержней из левой части в правую (рис. 2.8, б), то степень свободы не изменится, а получившаяся конструкция будет геометрически неизменяемой, поскольку она состоит из шарнирных треугольников.
|
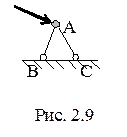
Очевидно, что подсчета степени свободы недостаточно. Он должен быть дополнен анализом геометрической структуры сооружения. Этот анализ состоит из рассмотрения расположения связей системы, в установлении порядка сочетания элементов. Рассмотрим простейшие законы образования геометрически неизменяемых систем.
1. Узел (материальную точку) можно присоединить к другому телу (земле) для создания геометрически неизменяемой системы при помощи двух стержней (рис. 1.9). При этом шарниры А, В и С не должны лежать на одной прямой.
|
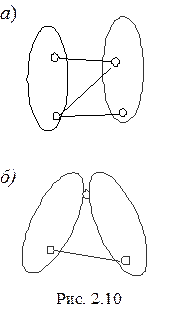
2. Два диска можно соединить в неподвижную конструкцию либо при помощи трех стержней (рис. 2.10, а), которые не должны быть параллельны друг другу и не пересекаться в одной точке, либо при помощи одного шарнира и одного стержня (рис. 1.10, б) (стержень и шарнир не должны лежать на одной прямой). В данном случае наглядно видно, что шарнир заменил две связи. В дальнейшем это качество одинарного шарнира будет использовано.
|
3. Три диска наиболее просто можно объединить в геометрически неизменяемую конструкцию при помощи трех шарниров (рис 2.11). При этом шарниры не должны лежать на одной прямой, в противном случае будем иметь мгновенно изменяемую конструкцию. На рис. 2.9, 2.10,б, и 2.11 показаны так называемые шарнирные треугольники, которые являются простейшей неизменяемой конструкцией и используются при создании более сложных конструкций.
|
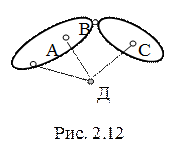
4. К двум дискам, соединенным шарниром, можно прикрепить узел при помощи трех стержней. При этом шарниры А, В и С не должны принадлежать одному диску (рис. 2.12).
|
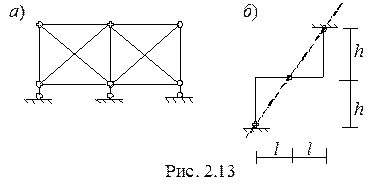
Как было указано выше, система может оказаться в положении так называемой мгновенной изменяемости, когда основные соединяющие шарниры находятся на одной прямой, либо опорные (связующие) стержни параллельны друг другу.
На рис. 2.13, а приведена дважды статически неопределимая ферма, которая является мгновенно изменяемой, поскольку опорные стержни параллельны. На рис. 2.13,б представлена статически определимая конструкция, состоящая из двух ломаных стержней. Если ломаные стержни представить как диски и в качестве третьего диска использовать опорное устройство (землю), то получим пример соединения трех дисков тремя шарнирами, лежащими на одной прямой. Это мгновенно изменяемая система, в которой невозможно найти опорные реакции. Если же изменить один из размеров одного ломаного стержня, шарниры не будут лежать на одно прямой и задача может быть решена.
Дата добавления: 2017-02-13; просмотров: 8143;
Поиск по сайту
Узнать еще
- Case-study (анализ конкретных ситуаций, ситуационный анализ)
- II Расчет и анализ трехфазных цепей
- II. Качественный контроль (социологический анализ).
- III и IV нейроны слухового пути. Третьи и четвертые нейроны слухового проводящего пути. Ядра слухового анализатора. Признаки поражения слухового пути.
- VII. Анализ характера
- І. Анализаторы І сигнальной системы
- ІІ. Анализаторы ІІ сигнальной системы
- Абсорбционный анализ по спектрам поглощения
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
