Действительная работа внутренних сил.

Для определения действительной работы внутренних сил (потенциальной энергии деформаций) выделим из заданной системы бесконечно малый элемент длиной dx (рис. 7.10, а) и приложим к нему усилия M, Q N, действующие на него со стороны отброшенных частей системы, и рассмотрим вызванные этими усилиями деформации (рис. 7.10. б).

Действительная работа внутренних усилий элемента, равных по величине и обратных по знаку усилиям M, Q N, составит:

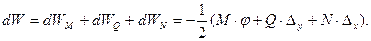
Знак «минус» объясняется здесь тем, что направление внутренних усилий элемента dx противоположно направлению его деформаций, в результате чего работа внутренних сил при загружении упругого тела всегда отрицательна.

Величины деформаций элемента определяются в соответствии с законом Гука по формулам

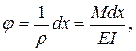
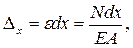
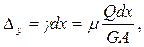(7.8)

где E и G – модули упругости материала соответственно 1 –го и 2- го рода, I и A – соответственно момент инерции и площадь поперечного сечения рассматриваемого стержня, m - коэффициент, учитывающий форму сечения стержня.

Суммируя элементарные работы по длине стержня, а затем по всем стержням системы, окончательно для работы внутренних сил системы получим:

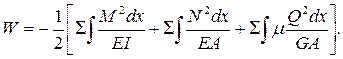(7.9)

Анализируя выражение (7.9), можно прийти к заключению, что потенциальная энергия деформации U = - W (см. выражение 7.7) всегда положительна, так как она выражается через квадраты внутренних усилий. По этой причине к вычислению потенциальной энергии неприложим принцип независимости действия сил, т. е. потенциальная энергия, вызванная действием группы сил, не равна сумме потенциальных энергий, вызванных каждой из сил в отдельности. Наконец, можно видеть, что в упругой системе суммарная работа внутренних (а также и внешних) сил определяется лишь конечным состоянием системы и не зависит от того, каким способом она пришла в это состояние (так как от этого не зависят значения M, Q, N).