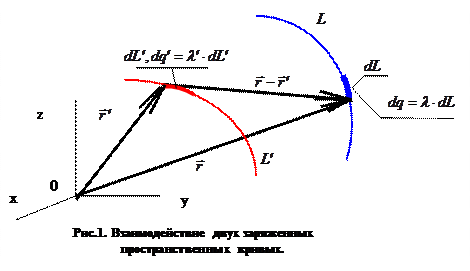
Взаимодействие двух заряженных пространственных кривых.

Пусть на пространственной кривой 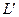, текущее положение точек которой описано с помощью радиус-вектора 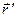, распределён электрический заряд с известной линейной плотностью 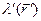. Элементарный отрезок 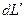кривой 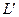содержит элементарных электрический заряд 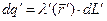. Пусть на пространственной кривой 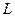, текущее положение точек которой описано с помощью радиус-вектора 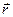, распределён электрический заряд с известной линейной плотностью 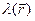. Элементарный отрезок 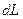кривой 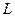содержит элементарный электрический заряд 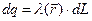. Пусть рассматриваемые пространственные кривые не имеют точек пересечения. Очевидно, что выделенные элементарные заряды (рис.1) можно рассматривать как точечные и применить для вычисления силы взаимодействия между ними закон Кулона:

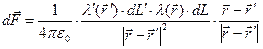. (1)

Соотношением (1) описана элементарная сила, действующая на электрический заряд 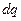«не штрихованного» элемента кривой 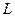со стороны элементарного электрического заряда 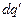, расположенного на «штрихованной» кривой 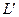. Зафиксируем, например, элементарный штрихованный заряд и вычислим силу его воздействия на все элементарные заряды не штрихованной кривой:

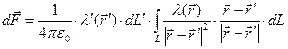. (2)

Теперь осталось просуммировать воздействие «всех» элементарных зарядов кривой 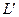на «все» элементарные заряды кривой :

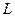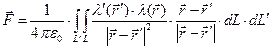. (3)

Располагая зависимостью (3), можно вычислить проекции рассматриваемой силы 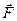на оси декартовой системы координат:

,

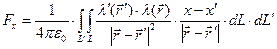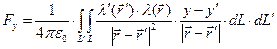,(4)

,

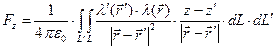где 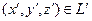, 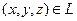. Используя зависимости (4), можно вычислить модуль силы электростатического взаимодействия и её направляющие косинусы.