ОБРАТИМОСТЬ ЧЕРТЕЖА. ОБРАЗОВАНИЕ ЭПЮРА

Чертеж, особенно технический, должен быть обратимым, т. е. должен давать возможность определить положение любой точки предмета либо относительно плоскости проекций, либо относительно другой данной точки. Это значит, что каждая точка, заданная на изображении, должна определять единственную точку изображенного объекта.

Если обратиться к черт. 1 или 2, то легко видеть, что проекция А' может рас­сматриваться не только как проекции точки А, но и как проекция точек А\, Ai и т. д., лежащих на проецирующей прямой А-А'. Поэтому полученное изображение пока не может нас удовлетворить.

Зададим плоскость проекции л и два направления проецирования s\ и S2 (черт 4). Точка А будет иметь две проекции: А' по направлению si и А" по направлению S2. Вторая точка В, расположенная на проецирующем луче А-А', по направлению si спроецируется точкой В', совпадающей с точкой А', но по направлению sz она спроецируется точкой В", отличной от точки А". Теперь по чертежу мы имеем

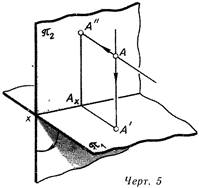
возможность сказать, что на нем изобра­жено две точки — А и В; кроме того, наличие двух проекций каждой из них позволяет определить положение их отно­сительно плоскости проекций и относитель­но друг друга. Действительно, если через точку А' провести прямую, параллельную направлению si, а через точку А" – прямую, параллельную направлению ss, то точка пересечения этих линий и будет данной точкой А (не пересечься эти прямые не могут, так как в противном случае точки А' и А" не могли бы быть проекциями одной точки). Подобным образом можно найти положение точки В и, следовательно, выяснить их взаимное расположение.

Итак, наличие двух проекций объекта может сделать чертеж обратимым.

Получить два изображения на одной плоскости при ортогональном проецирова­нии нельзя, так как нельзя задать два отличных друг от друга направления проецирования. Поэтому проецирование производится на две плоскости проекций – Я1 и яз. Располагаются они взаимно перпендикулярно (черт. 5), причем плоскость Л1 – горизонтально и называется поэтому горизонтальной плоскостью проекций, а плоскость-па – перед наблюдателем. Ее называют фронтальной плоскостью проекций. После проецирования на них объекта плоскости ni и Я2 вращением вокруг линии их пересечения совмещают друг с другом, образуя одну плоскость чертежа.

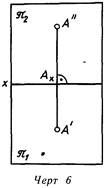
Развернутое изображение обычно называют эпюром* (черт. 6) Линия пересечения плоскостей проекций называется осью проекций и обозначается на эпюре буквой х. Применение для построения чертежа метода ортогонального проецирования было предложено французским ученым Гаспаром Монжем (1746-1818), что послужило основанием назвать этот метод методом Монжа, а описанный выше эпюр эпюром Монжа

На эпюре проекции , каждой изображаемой точки располагаются на прямой линии, называемой линией проекционной связи докажем, что она пер­пендикулярна к оси проекций

Проецирующие прямые А-А' и А-А" (см черт. 5) образуют плоскость, перпендикулярную к плоскостям Я1 и па и, следовательно, к оси х. Но если ось х перпендикулярна к плоскости AA'A", то она перпендикулярна к любой прямой этой плоскости, т. е. и к прямым Ax-А' и А^-А" В одной же точке Ах на эпюре можно восставить единственный перпендикуляр к оси х – линию А'-Ац-А" или А'-А".

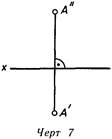
Если не ограничивать плоскости проекций, то эпюр будет иметь вид черт. 7.

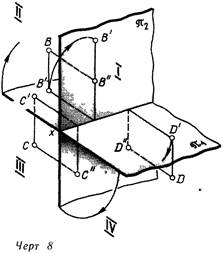
Две плоскости проекций делят пространство на четыре четверти (черт 8), при этом плоскости, естественно, считаются безграничными Плоскости делят друг друга на «полуплоскости», или «полы» (верхняя пола, нижняя, передняя и задняя) Четверти или, как их еще называют, квадранты нумеруют в соответствии с черт. 8.

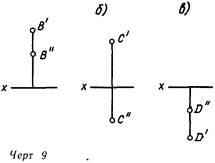
Обычно изображаемый объект помещают в первой четверти (точка А, черт 5-7), но встречаются случаи, когда некоторые его элементы оказываются расположенными и в других четвертях Поэтому ознакомимся с эпюрами точек, лежащих во II, III и IV четвертях.

Точка В (черт. 8 и 9, а) находится во 2 четверти. Ее фронтальная проекция будет на верхней поле плоскости V и на эпюре выше оси х. Горизонтальная ее проекция лежит на задней поле плоскости H и после совмещения последней с плоскостью ля окажется тоже выше оси х Точка С (черт. 8 и 9, б), расположенная в III четверти, спроецируется на нижнюю полу фронтальной плоскости и на заднюю полу горизонтальной, поэтому ее проекция С" будет на эпюре ниже оси х, а проекция С' – выше Обе проекции точки D, находящейся в IV четверти, на эпюре лежат ниже оси х (черт. 9, в).

Вернемся опять к черт. 5 и, сравнивая его с черт. 6, заметим, что фигура AA'AxA" – прямоугольник, и на эпюре отрезки [А'-А,}=[А-А"} и [А"-А,]= =[А-Л'] выражают собой расстояния оригинала А соответственно от фронтальной и горизонтальной плоскостей проекций. Следовательно, положение точки А по отношению к плоскостям H и Y вполне определено заданием двух ее проекций. Несмотря на это в практике в ряде случаев целесообразно строить дополнитель­ные проекции объектов.

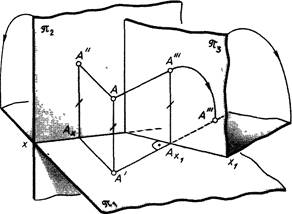
Новую плоскость проекций располагают перпендикулярно к одной из данных плоскостей проекций. На черт. 10 введена дополнительная плоскость проекций яз, пер­пендикулярная к плоскости Я|. Построена третья проекция А'" данной точки А, после чего плоскость яз совмещена с горизонтальной плоскостью Я1 вращением вокруг линии их пересечения. Очевидно, при этом образуется дополнительный эпюр Монжа с осью х\. На этом эпюре проекции точки А

связаны линией проекционной связи Л'— А'", перпендикулярной к оси х\, а отрезки [A'—Ajq] и, [А'"—Ах\\ выражают рас­стояния точки А соответственно от плос­костейW и H.

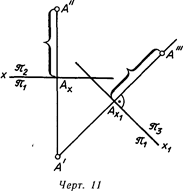
На черт. 11 точка А задана проекциями А' и А" в системе плоскостей проекций Я1/Я2. Введением дополнительной плос­кости W образована система плоскостей проекций H/W с осью х\ и построена третья проекция точки А. При построении через А' проведена линия проекционной связи, перпендикулярная к оси х\, и на ней от точки Ax^ отложено расстояние точки А от плоскости H, которое задано в системе плоскостей H/Y отрезком [А"—АЛ:

[А"-А^] = [А'"-АЛ.

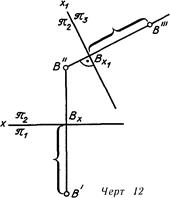
На черт. 12 построена третья проекция точки В на плоскости W, перпендикулярной к плоскости V. Для этого через точку В"

проведена линия проекционной связи, пер­пендикулярная к новой заданной оси проекций х\ и от точки B на ней отложено расстояние точки В от плоскости V. В за­данной системе плоскостей проекций V/H оно равно отрезку [В'—Вх].

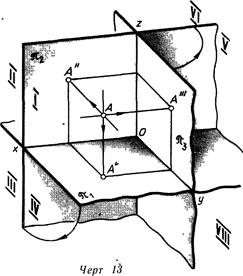
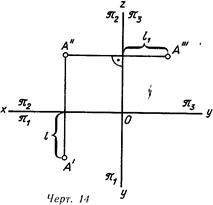
Наиболее часто используют третью плос­кость проекций, перпендикулярную к двум данным: W перпендикулярна H, W перпендикулярна V (черт. 13). Такую плоскость называют профильной плос­костью проекций. Она пересекается с плоскостью H по линии у, а с плоскостьюV— по линии z. Принято совмещать эту плоскость с плоскостью чертежа вра­щением ее вокруг вертикальной линии z. При этом получается эпюр, показанный на черт. 14. Третью проекцию точки строят так же, как это было сделано на черт. 12:

проводят линию проекционной связи А"— А'", перпендикулярную к оси z, и на ней от этой оси откладывают отрезок, равный расстоянию точки А от плоско­сти эт2, величина которого определяется положением горизонтальной проекции точ­ки А (/!=/).

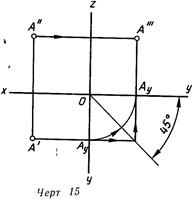
Точку А'" можно также получить в пе­ресечении двух линий проекционной свя­зи — линии А" —А'" системы V/W и линии А'—А'" системы H/W (черт. 15). Вторая линия состоит из двух отрезков, что явля­ется следствием принятого правила раз­вертывания в плоскость трехгранного уг­ла, образованного плоскостями H, V и W. Отрезок [А'—Ау] перпендикулярен к изо­бражению оси у на плоскости H (горизон­тален), а отрезок [Ay—А'"] перпендику­лярен к изображению оси у на плоскости W (вертикален). Тождество точек Ау может-быть показано дугой окружности, соеди­няющей их.

При необходимости показать на чер­теже порядок построения отдельных то­чек можно пользоваться еще свойством отрезков линии связи A''—А'"' пересе­каться на некоторой прямой, проходящей через точку О и составляющей с гори­зонтальной линией угол 45° (ее называют постоянной прямой чертежа). Для этой же цели на линиях проекционной связи наносят стрелки.

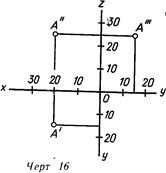
Линии пересечения взаимно перпен­дикулярных плоскостей проекций могут быть приняты за оси координат. В связи с этим их обозначают буквами х, у и z. В отличие от системы ( координат, приме­няемой в математике, в данной системе положительные величины на оси х откла­дывают влево от начала координат — точки О. Выбрав ту или иную величину масштабной единицы, можно построить проекции точек по заданным численным значениям их координат. На черт. 16 построены проекции точки. А, имеющей абсциссу х, равную 20 единицам измере­ния, ординату у, равную 15 единицам, и аппликату z, равную 25 единицам. Короче это записывается так: Л (20, 15, 25).

Три плоскости проекций делят прост­ранство на восемь частей, называемых октантами. Нумерация их показана на черт. 13. Как отмечалось выше, мы будем помещать изображаемый объект в первой четверти или в первом октанте. Так при­нято делать в СССР и в странах Европы. При составлении чертежей в странах Американского континента объект поме­щают в VII октанте. В европейской проекции объект помещен между наблюда­телем и каждой плоскостью проекций, в американской—плоскости проекций отделяют объект от наблюдателя.

ПРОЕКЦИИ ПРЯМЫХ ЛИНИЙ